Le sens des mathématiques 20231020

Michel Damiens
mail : michel.damiens@gmail.com
site web : utl.manthano.fr
Ce site s’affiche en mode diapo : pour passer d’une page à la suivante ou à la précédente utiliser les touches « flèche droite » ou « flèche gauche » de votre clavier.
Pour le moment il est « en construction » avec de nombreux « bugs » : par exemple les menus risquent de ne pas fonctionner correctement.
Histoire de ce cours

(Merci à Jean-Luc Mauriet pour ses commentaires graphiques)
Le « sens des mathématiques »

j’avais donné à ces cours au départ le titre : le sens des mathématiques, en référence au titre d’un livre d’un de mes maîtres : Faire des mathématiques : le plaisir du sens
Il s’agit à la fois :
⏵du sens de l’histoire des mathématiques (progrès ou progression),
⏵du sens qu’acquièrent les mathématiques au cours de cette histoire,
⏵et surtout du sens que ces mathématiques confèrent à notre rapport au réel.
Tout ceci concourant peut-être pour l’auditeur à acquérir un certain « sens des mathématiques ».
De L’histoire des mathématiques à Histoire(s) de(s) mathématique(s)
Les années précédentes, j’ai détaillé l’évolution des mathématiques depuis l’Antiquité grecque jusqu’au XVIIème siècle.
Les limites de cette méthode d’exposition : à partir de la fin du XVIIème siècle, les contenus mathématiques deviennent de plus en plus « techniques »
Travailler sur des thèmes :
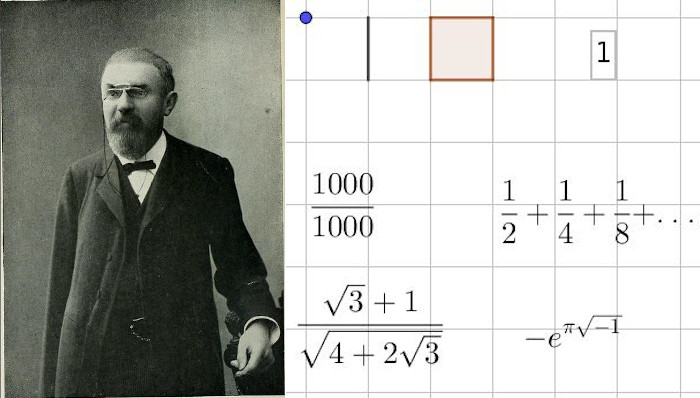
- qu’est-ce qu’un nombre ?
- la symétrie
- quelles géométries pour notre monde ?
- les certitudes du hasard
- ...
Objectifs
Comprendre l’activité mathématique
Essayer de décrire l’activité mathématique en développant certains « thèmes » parmi ceux qui ont été présents tout au long de son histoire.
Les thèmes choisis sont en grande partie liés à mes propres intérêts dans la matière et surtout à mes connaissances et capacités de compréhension qui restent bien limitées par rapport à la richesse et à la complexité de l’ensemble de ce qui a été produit jusqu’ici dans ce domaine.
Susciter le plaisir de comprendre
La méthode d’exposition pourra être parfois impressionniste, parfois détaillée, en fonction des sujets traités.
Je souhaiterais que vous toutes et tous qui suivez ce cours y trouvent de l’intérêt et surtout du plaisir, indépendamment des connaissances préalables dont vous disposez.
Les questions, les discussions sont absolument nécessaires, je dirais presque obligatoires : vous vous devez de m’interrompre et me questionner à tout moment si vous avez besoin d’éclaircissements ou pour apporter des compléments ou des critiques à ce que j’expose.
Aborder les problématiques passées et contemporaines
J’essaierai, en ne me cantonnant pas comme par le passé à un exposé historique plutôt linéaire, de vous faire toucher du doigt certains développements récents (au cours de XXème siècle) du travail des mathématiciens.
Les exemples que je vais développer sont supposés vous permettre de vous faire une opinion sur les questions qui se posent en mathématiques et sur les mathématiques, questions dont je vais aborder aujourd’hui quelques-uns des aspects.
Introduction
de quoi les mathématiques sont-elles le nom ?
Qu’est-ce que les mathématiques ?
La mathématique est l’art de donner le même nom à des choses différentes.
(Henri Poincaré) Science et méthode, 1908
Depuis quand fait-on des mathématiques ?
L’os d’Ishango

prémices d’activité calculatoire ?
Mésopotamie

À partir du VIIIème millénaire av. J.-C. les « calculi » permettaient de transmettre des informations numériques permettent de compatbiliser des biens. Ils sont contemporains de l’invention de l’écriture.
Le « miracle » grec
Au VIème siècle av. J.-C. en Asie Mineure puis en Grèce continentale, s’amorce une révolution qui marque la naissance de ce qui constitue actuellement les mathématiques :
■ la conceptualisation des objets mathématiques (formes et nombres)
■ la démonstration qui articule logiquement ces concepts (Euclide)
Quelques questions philosophiques
Platon (-428 à -348)

Écrit au frontispice du lycée, cela semble signifier que les mathématiques sont une condition nécessaire pour la réflexion philosophique. Elles sont le moyen privilégié d’accès aux Idées.
Galilée (1564-1642)

« La philosophie est écrite dans cet immense livre qui continuellement reste ouvert devant les yeux (ce livre qui est l’Univers), mais on ne peut le comprendre si, d’abord, on ne s’exerce pas à en connaître la langue et les caractères dans lesquels il est écrit. II est écrit dans une langue mathématique, et les caractères en sont les triangles, les cercles, et d’autres figures géométriques, sans lesquelles il est impossible humainement d’en saisir le moindre mot; sans ces moyens, on risque de s’égarer dans un labyrinthe obscur. » [L’Essayeur (Il Saggiatore) - 1623]
Il semble ici que Galilée déclare que la philosophie, c’est à dire le système de pensée ayant pour but de comprendre le monde, s’écrit en utilisant le langage mathématique.
À partir de là, avec Descartes, Leibniz, Kant, Husserl et jusqu’à notre époque on a tendance à considérer que les mathématiques sont le modèle, la clé d’intelligibilité du monde (de la nature).
Les enjeux
La primauté des mathématiques dans la conception platonicienne est contestée par Aristote. De manière générale on peut concevoir plusieurs positions différentes concernant le statut des mathématiques
- les mathématiques constituent une réalité en soi
- il s’agit d’un mode d’accès à la réalité, elles existent uniquement dans la pensée (des mathématiciens)
- il s’agit d’un langage et d’une logique (philosophie analytique)
Mais ceci soulève en fait la question de la nature de la réalité et du mode d’existence des objets mathématiques.
Les mathématiques sont-elles une science ?
L’épistémologue Karl Popper (1902-1994) caractérise le travail scientifique en utilisant l’idée de réfutabilité (ou falsiabilité) par l’expérience.
Est-ce seulement un exercice intellectuel « gratuit » ou est-ce une science ?
Le travail mathématique, de part sa créativité, s’apparente aussi à l’art.
Quelques types d’objets et grandes structures du corpus mathématique
Les démonstrations portent sur des objets et des structures qui les relient.
Par exemple les nombres (arithmétique, discret), le continu (la forme, géométrie) sont deux types d’objets qui vont s’articuler à travers des structures (ensemble, fonctions, groupes, espaces vectoriels, catégories...) sur lesquelles vont porter les démonstrations. Le travail mathématique du dernier siècle consiste souvent en la mise en relation des objets à travers ces structures et la mise en relation de ces structures.
Preuves
On doit être capable de dire d’un énoncé mathématique s’il est vrai ou faux.
Il est assez facile de se mettre d’accord sur ce qu’on entend pas preuve (encore que, dans la pratique, les preuves sont accompagnées de commentaires métamathématiques qui rendent parfois difficile de s’assurer de leur validité, en particulier si ses commentaires introduisent des éléments sémantiques).
En pratique on dira qu’une preuve est un argument mathématique convaincant suffisamment détaillé qui établit logiquement la conclusion d’un théorème à partir de ses hypothèses.
La validité d’une preuve est aussi un phénomène social : elle dépend en dernier ressort de l’avis de la communauté mathématique.
L’intervention de l’informatique dans les démonstrations (théorème des 4 couleurs) et les logiciels de vérification des preuves (Coq, Mizar, Isabelle).
Fonctions de la preuve
- la preuve qui sert à (se) convaincre de la vérité
- la preuve qui sert à comprendre (à « voir »)
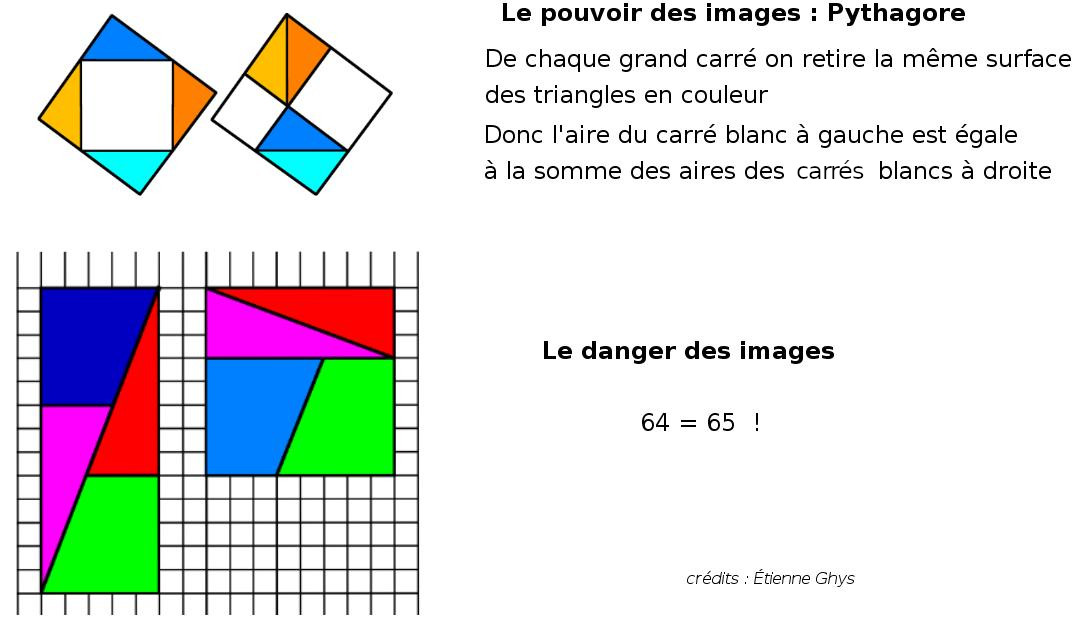
Preuve par image
Vérité

« Ce qui limite le vrai, ce n’est pas le faux, c’est l’insignifiant » (René Thom)
« Même pas faux » (Wolfgang Pauli, au sujet d’un article de physique sans intérêt) L’expression « même pas faux » est utilisée pour qualifier les théories contestables, celles dont il n’est pas possible de dire si elles sont vraies ou fausses. Ces théories ne satisfont pas aux critères de réfutabilité énoncés par Karl Popper qui dit que les hypothèses scientifiques doivent pouvoir être testées.
La preuve est du côté syntaxique, la vérité du côté sémantique.
La question de la vérité d’un énoncé mathématique est beaucoup plus complexe que celle de sa démonstrabilité.
Le théorème d’incomplétude de Gödel.
Qu’est-ce qu’un conjecture ?

Les conjectures apparaissent et se multiplient surtout au début du XXème siècle, à l’époque où se développe le structuralisme.
Même si on qualifie de conjecture le théorème énoncé par Fermat, Gauss en dit par exemple dans une lettre à Olbers que c’est un énoncé insignifiant. Il ajoutera quand même que son importance à ses yeux vient de ce qu’il a nécessité (pour Gauss) une reconstruction du champ arithmétique.
Conjecture et hypothèse
Une conjecture n’est pas une simple hypothèse. Elle doit à la fois mettre en relation plusieurs champs distincts des mathématiques, susciter la constitution d’une communauté de mathématiciens qui y travaillent, et éventuellement avoir été validée sur de nombreux cas particuliers. C’est le cas, par exemple, de la conjecture de Riemann qui relie la distribution des nombres premiers aux solutions d’une équation analytique :
\(\zeta(s)=0\) avec \(\zeta(s)=1+\cfrac{1}{2^s}+\cfrac{1}{3^s}+\cfrac{1}{3^s}+\cfrac{1}{4^s}+\ldots= \cfrac{1}{\left(1-\cfrac{1}{2^s}\right)\times\left(1-\cfrac{1}{3^s}\right)\times\left(1-\cfrac{1}{5^s}\right)\times\left(1-\cfrac{1}{7^s}\right)\times\left(1-\cfrac{1}{11^s}\right)\times\ldots}\)
La « croyance » en la vérité des conjectures est souvent renforcée par la démonstration d’une de ses conséquences.
Toutefois, savoir que A implique B et que B est vrai ne permet pas de conclure que A est vrai.
Un exemple de conjecture fausse
En 1769, Euler énonce la conjecture suivante :
Si une puissance \(n^{ième}\) (d’un entier \(x\)) se décompose en somme de puissances \(n^{ièmes}\) d’entiers, alors cette somme contient au moins \(n\) termes.
Autrement dit : si
\(x^n=a_1^n+a_2^n+\ldots+a_k^n\) alors \(k\geq n\)
C’est seulement en 1966 que Lander et Parkin trouvent un contre-exemple, en utilisant l’informatique :
\(27^5+84^5+110^5+133^5=144^5\)
Mathématiques et liberté

Georg Cantor (1845-1918) : « l’essence des mathématiques c’est la liberté »
Faire des mathématiques, c’est se les approprier, sans prendre rien à personne. Une fois qu’on a compris la preuve de ce qu’on appelle Théorème de Pythagore sur les triangles rectangles, l’aide extérieure n’est plus nécessaire et l’on se sent libre de point de se considérer comme coauteur [...]
La liberté fait également partie de l’enseignement dispensé par des mathématiciens qui, au moins, facilite la maîtrise du discours sur les calculs concernant les outils de politique
gouvernance, sous forme de statistiques, de prévisions, de risques, etc.
[Jean Dhombres]
Les hommes sont soumis aux contraintes de leur environnement.
De tous temps ils ont essayé de gérer ces contraintes à l’aide de représentations imaginaires : mythes, religions, ...
Les mathématiques sont l’un des outils inventés par l’homme pour répondre à ses questions.
Elles mettent en œuvre la capacité humaine à user de son imagination tout en se pliant à des règles très strictes.
Cartographies du monde mathématique
Mathématistan
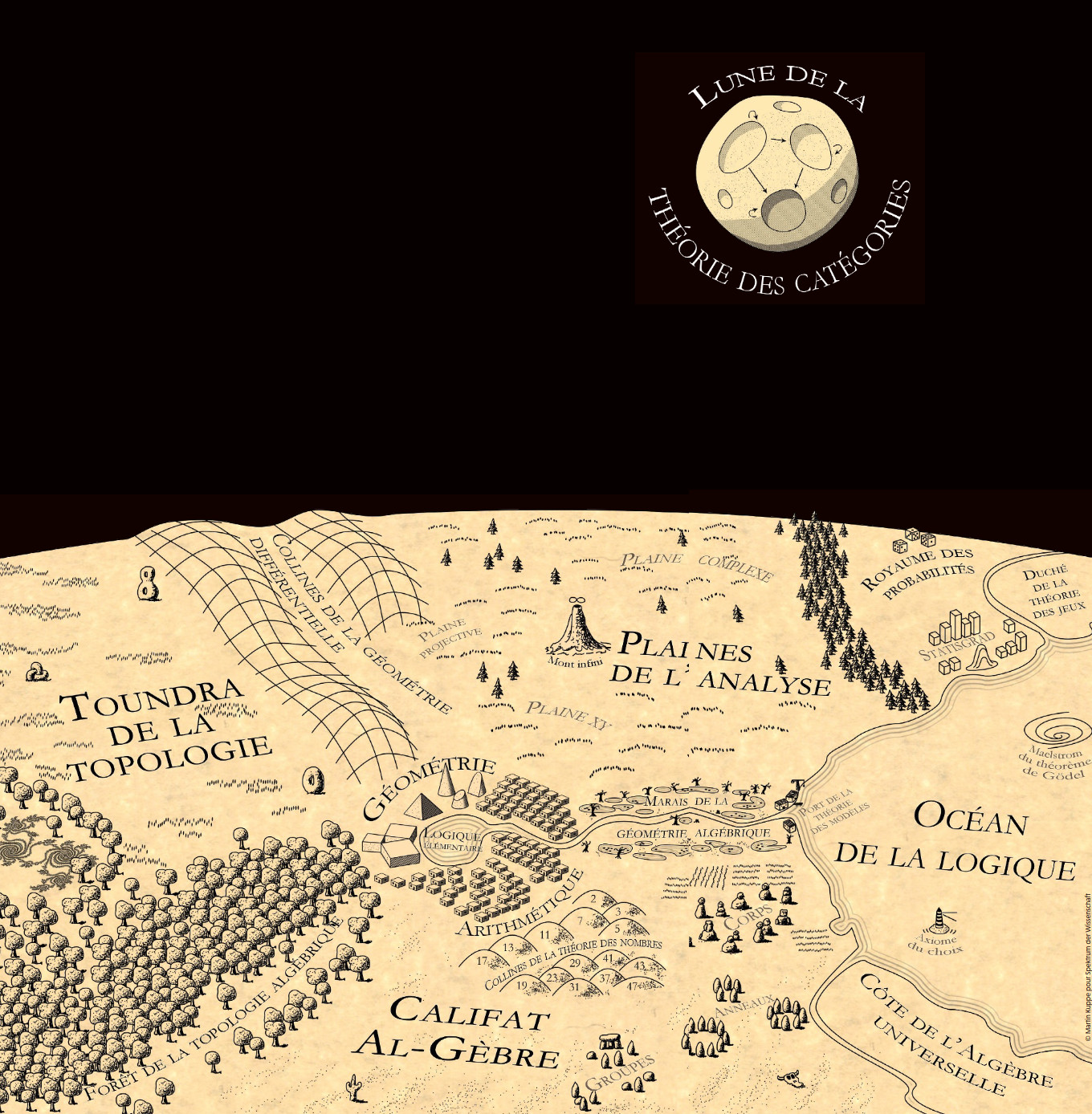
René Thom : tableau des mathématiques
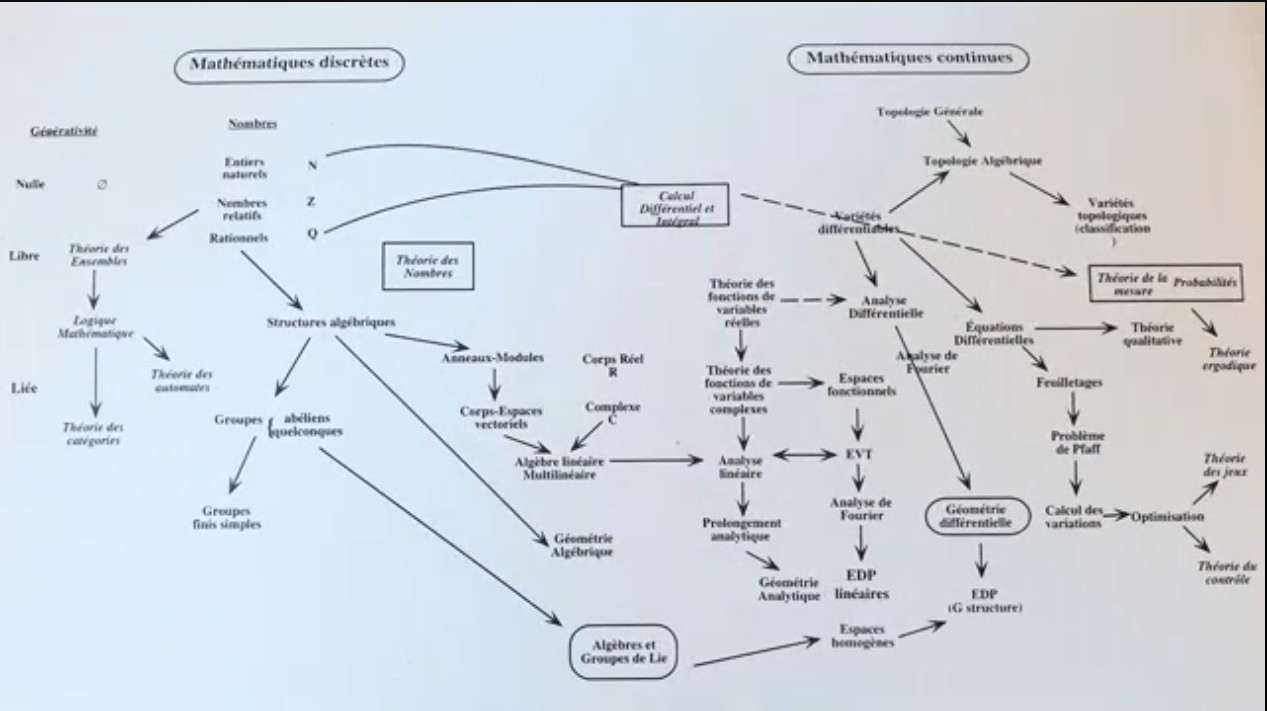
René Thom : carte du sens
Le(s) génie(s) des mathématiques

Les mathématiques, qu’elles soient découvertes ou inventées, sont produites par des mathématiciens dont le façon de travailler et la manière de concevoir les concepts et les outils peuvent varier considérablement.
Trois exemples de grands mathématiciens dont les démarches sont très différentes : Galois, Ramanujan, Grothendieck
Évariste Galois (1811-1832)

En s’attaquant au problème général de la résolution des équations algébriques, Galois ne va pas chercher à trouver les solutions. Il va analyser globalement l’ensemble S des solutions et surtout le groupe des symétries de S. C’est la structure de ce groupe qui va déterminer la condition de résolubilité (par radicaux) de l’équation.
Srinivasa Ramanujan (1887-1920)

G. H. Hardy, concernant la lettre que Ramanujan lui avait envoyée en 1913 dit : les formules qu'elles contenaient ne pouvaient qu'être justes, car personne n'aurait eu une imagination suffisante pour les inventer et qu'elles soient fausses.
Et aussi : Ramanujan travaillait par induction à partir d'exemples numériques, beaucoup plus que ne le faisait la majorité des mathématiciens contemporains …; mais, en alliant sa mémoire, sa patience et sa puissance de calcul, il aboutissait à une capacité de généralisation, une appréciation des formes, et une flexibilité pour de rapides modifications de ses hypothèses, qui étaient souvent surprenantes et le rendait sans rival à ce jour dans son domaine de compétence.
Alexandre Grothendieck (1928-2014)

_Quelques citations, extraites de Récoltes et semailles_ :
Mais comme son nom même le suggère, un « point de vue » en lui-même reste parcellaire. Il nous révèle un des aspects d’un paysage ou d’un panorama, parmi une multiplicité d’autres également valables, également « réels ». C’est dans la mesure où se conjuguent les points de vue complémentaires d’une même réalité, où se multiplient nos « yeux », que le regard pénètre plus avant dans la connaissance des choses. Plus la réalité que nous désirons connaître est riche et complexe, et plus aussi il est important de disposer de plusieurs « yeux » pour l’appréhender dans toute son ampleur et dans toute sa finesse.
(suite)
C’est dire que s’il y a une chose en mathématique qui (depuis toujours sans doute) me fascine plus que toute autre, ce n’est ni « le nombre », ni « la grandeur », mais toujours la forme. Et parmi les mille-et-un visages que choisit la forme pour se révéler à nous, celui qui m’a fasciné plus que tout autre et continue à me fasciner, c’est la structure cachée dans les choses mathématiques. La structure d’une chose n’est nullement une chose que nous puissions « inventer ». Nous pouvons seulement la mettre à jour patiemment, humblement en faire connaissance, la « découvrir ». S’il y a inventivité dans ce travail, et s’il nous arrive de faire œuvre de forgeron ou d’infatigable bâtisseur, ce n’est nullement pour « façonner », ou pour « bâtir », des « structures ». Celles-ci ne nous ont nullement attendues pour être, et pour être exactement ce qu’elles sont ! Mais c’est pour exprimer, le plus fidèlement que nous le pouvons, ces choses que nous sommes en train de découvrir et de sonder, et cette structure réticente à se livrer, que nous essayons à tâtons, et par un langage encore balbutiant peut-être, à cerner.
Ce qui fait la qualité de l’inventivité et de l’imagination du chercheur, c’est la qualité de son attention, à l’écoute de la voix des choses. Car les choses de l’Univers ne se lassent jamais de parler d’elles-mêmes et de se révéler, à celui qui se soucie d’entendre. Et la maison la plus belle, celle en laquelle apparaît l’amour de l’ouvrier, n’est pas celle qui est plus grande ou plus haute que d’autres. La belle maison est celle qui reflète fidèlement la structure et la beauté cachées des choses.
Le simple fait d’écrire, de nommer, de décrire – ne serait-ce d’abord que décrire des intuitions élusives ou de simples « soupçons » réticents à prendre forme – a un pouvoir créateur.
Les ruptures dans l’histoire des mathématiques
Exemples
- la découverte de l’irrationalité dans les mathématiques grecques
- racine carrée de -1 (XVIème siècle) : Cardan, Bombelli
- les sommes infinies (XVIIème-XVIIIème siècle) : Newton, Euler
- les géométries non euclidiennes (milieu XIXème siècle) : Lobatchevski, Bolyai
- l’infini actuel (fin XIXème siècle) : Cantor
- les énoncés indécidables : Gödel
Analyses
Felix Klein en 1926 analyse la rupture que constitue le passage du XVIIIème au XIXème siècle en terme de rigueur et d’abstraction.
Il en donne aussi des raisons socio-politiques ; pour Felix Klein, cette mutation intellectuelle est étroitement liée aux changements sociaux provoqués par la Révolution française : la démocratisation de l’accès aux sciences, la spécialisation scientifique, la professionnalisation de l’enseignement.
Dans ce cadre, l’École polytechnique de Paris apparaît emblématique de tous ces changements, avec une formation des cadres civils et militaires sur la base d’une éducation mathématique de haut niveau ; Felix Klein souligne que l’École polytechnique, par ses enseignants et ses anciens élèves, est à l’origine de presque toutes les grandes nouveautés scientifiques qui surviennent en France dans les premières décennies du XIXème siècle.
Quelques références : Thomas Kuhn, La structure des révolutions scientifiques, 1962
Imre Lakatos, Preuves et réfutations, 1984
Esthétique et plaisir
Citations
Henri Poincaré
On peut s’étonner de voir invoquer la sensibilité à propos de démonstrations mathématiques, qui, semble-t-il, ne peuvent intéresser que l’intelligence. Ce serait oublier le sentiment de la beauté mathématique, de l’harmonie des nombres et des formes, de l’élégance géométrique. C’est un véritable sentiment esthétique que tous les vrais mathématiciens connaissent. Et c’est bien là de la sensibilité. [...] Cette harmonie est à la fois une satisfaction pour nos besoins esthétiques et une aide pour l’esprit, qu’elle soutient et qu’elle guide. Et, en même temps, en mettant sous nos yeux un tout bien ordonné, elle nous fait pressentir une loi mathématique. […] Les combinaisons utiles, ce sont précisément les plus belles, je veux dire celles qui peuvent le mieux charmer cette sensibilité spéciale que tous les mathématiciens connaissent, mais que les profanes ignorent au point qu’ils sont souvent tentés d’en sourire.
[Science et méthode, 1908, Henri Poincaré]
Cette harmonie que l’intelligence humaine croit découvrir dans la nature, existe-t-elle en dehors de cette intelligence ? Non, sans doute, une réalité complètement indépendante de l’esprit qui la conçoit, la voit ou la sent, c’est une impossibilité. Un monde si extérieur que cela, si même il existait, nous serait à jamais inaccessible. Mais ce que nous appelons la réalité objective, c’est, en dernière analyse, ce qui est commun à plusieurs êtres pensants, et pourrait être commun à tous ; cette partie commune, nous le verrons, ce ne peut être que l’harmonie exprimée par des lois mathématiques. C’est donc cette harmonie qui est la seule réalité objective, la seule vérité que nous puissions atteindre ; et si j’ajoute que l’harmonie universelle du monde est la source de toute beauté, on comprendra quel prix nous devons attacher aux lents et pénibles progrès qui nous la font peu à peu mieux connaître.
[La Valeur de la science, Henri Poincaré, 1911]
Le savant n’étudie pas la nature parce que cela est utile ; il l’étudie parce qu’il y prend plaisir et il y prend plaisir parce qu’elle est belle. Si la nature n’était pas belle, elle ne vaudrait pas la peine d’être connue, la vie ne vaudrait pas la peine d’être vécue. Je ne parle pas ici, bien entendu, de cette beauté qui frappe les sens, de la beauté des qualités et des apparences ; non que j’en fasse fi, loin de là, mais elle n’a rien à faire avec la science ; je veux parler de cette beauté plus intime qui vient de l’ordre harmonieux des parties, et qu’une intelligence pure peut saisir.
[Science et méthode, 1908, Henri Poincaré]
et d’autres...
Il me semble maintenant que les mathématiques sont capables d’une excellence artistique aussi grande que celle de n’importe quelle musique, peut-être plus grande ; non pas parce que le plaisir qu’elles procurent (quoique très pur) soit comparable, soit en intensité, soit en nombre de personnes qui l’éprouvent, à celui de la musique, mais parce qu’elles donnent dans une perfection absolue cette combinaison, caractéristique du grand art, de la liberté divine, avec le sentiment d’un destin inévitable ; car, en fait, elles construisent un monde idéal où tout est parfait mais vrai.
[Bertrand Russell (1872-1970), Autobiographie]
Question à Cédric Villani : Les mathématiciens sont attachés à la beauté des mathématiques. Poincaré disait : « Une théorie est bonne quand elle est belle. » Que vient faire ici la beauté ?
Cédric Villani :
C’est beau quand ça amène un élément de surprise, quand survient une rencontre des éléments de sphères diverses. On peut y voir une analogie avec la beauté orchestrale. Poincaré voyait une harmonie dans la rencontre des concepts. Les mathématiciens ont cette idée que c’est en cherchant dans la direction la plus belle que l’on a le plus de chances de trouver quelque chose, et je l’ai expérimenté plusieurs fois. On serait perdu dans l’océan des possibles sans l’esthétique pour nous guider. Les mathématiciens parlent sans cesse d’une belle preuve, d’une jolie solution…
« Il n’est pas possible d’être mathématicien sans avoir l’âme d’un poète. [...] le poète doit seulement voir ce que les autres ne discernent pas, son regard doit pénétrer plus profondément, et il en est de même pour le mathématicien »
Sofia Vasilyevna Kovalevskaya
La beauté comme guide
Dirac : entre une équation de la physique considérée comme belle et un fait de la physique, une expérience qui viendrait à contredire cette équation, je choisis l’équation
Thomas Huxley (biologiste, père d’Aldous Huxley) : Quand même, on ne va pas sacrifier nos merveilleuses théories pour un misérable fait qui les contredit !
Hermann Weyl : mon travail a toujours consisté à unir la vérité et la beauté, mais quand j’ai eu à choisir l’une ou l’autre, j’ai toujours choisi la beauté.
(et ses erreurs : Kepler et les polyèdres réguliers)
Hermann Weyl et Henri Poincaré insistent sur le rôle de la symétrie dans le sentiment esthétique. Cette symétrie au sens large que lui donnent les mathématiques à travers la théorie des groupes est au coeur des théories depuis Évariste Galois et Felix Klein ; elle est aussi devenue l’un des outils fondamentaux de la physique théorique au XXème siècle.
Parmi les critères esthétiques, la simplicité occupe une place particulière dans le choix des axiomes : le cinquième postulat d’Euclide paraît problématique parce qu’il semble artificiel, trop peu évident.
Belles formules
\(e^{i\pi}=-1\) (Euler)

\(S - A + F = 2\) (Euler)
Beauté mathématique dans la nature

tournesol (Fibonacci), flocon de neige, ...
Vidéo (Robert Gergondey)
Les maths, à quoi ça sert ?

Exercices (série 1)
Les exercices que je propose sont en général en relation avec le cours du jour ou en préparation du suivant.
Vous pouvez m’envoyer vos réponses, vos essais, vos questions ... à michel.damiens@gmail.com avant le cours suivant. J’y répondrai en vous indiquant si la votre réponse est exacte ou en vous donnant des informations supplémentaires pour vous aider à continuer à chercher.
Cette semaine il s’agit de vous préparer à la suite qui va concerner l’arithmétique.
Exercice 1.1 : démontrer que tout nombre impair est la différence de 2 carrés d’entiers (par exemple 11 = 6² - 5²) ; est-ce vrai pour les nombres pairs ? (donner des exemples)
Exercice 1.2 : trouver tous les nombres entiers \(x\), \(y\) tels que \(xy+x+y=492\)
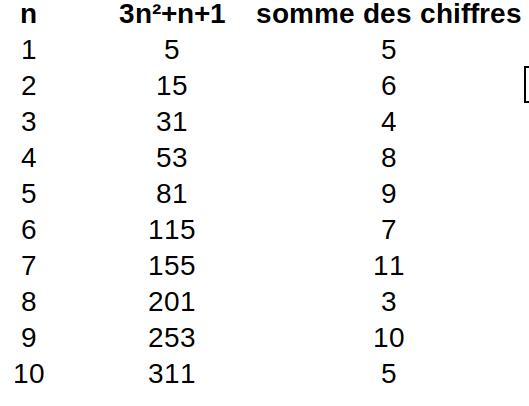
Exercice 1.3 : existe-t-il un entier n tel que la somme des chiffres (en base 10) de 3n²+n+1 soit inférieure ou égale à 2 ?
Solutions
Exercice 1.1
C’est évident si on utilise la représentation des carrés de Pythagore et qu’on examine les gnomons qui permettent de passer d’un carré au suivant.
Sinon voici une démonstration « algébrique » :
Soit un nombre \(k\) différence de 2 carrés : on peut écrire \(k = x^2 - y^2\) ce qui donne \(k = (x - y)(x + y)\) ;
on a en particulier la solution \(x - y = 1\) et \(x + y = k\), ce qui donne \(2x = k + 1\) et \(2y = k - 1\) soit \(x = \cfrac{k+1}{2}\) et \(y = \cfrac{k-1}{2}\) qui sont des entiers si \(k\) est impair.
Si \(k\) est pair, au moins l’un des deux facteurs \(x-y\) ou \(x+y\) est pair ; or \(x+y=x-y+2y\) et \(x-y=x+y-2y\) donc les deux facteurs sont pairs.
Il faut donc que \(k\) soit un multiple de 4.
Mais est-ce suffisant ? Oui en remarquant que \(k=4p=(p+1)^2-(p-1)^2\)
C’est vrai pour les nombres pairs multiples de 4.
autre explication : \((n+1)^2=n^2+2n+1\). On passe donc d’un carré au suivant en ajoutant un nombre impair.
En itérant, on voit qu’une différence de deux carrés est une somme de nombres impairs consécutifs.
Mais deux nombres impairs consécutifs ont une somme multiple de 4 (car \(2k+1+2k+3=4k+4\)).
conclusion : tout nombre qui n’est pas de la forme \(4p+2\) est une différence de 2 carrés
remarque : la formule obtenue ci-dessus \(k=\left(\cfrac{k+1}{2}\right)^{2}-\left(\cfrac{k-1}{2}\right)^{2}}\) montre que toute fraction positive et différente de 1 est la différence des carrés de 2 fractions non nulles ;
mais est-ce que toute fraction positive est la somme des carrés de 2 fractions non nulles ?
Exercice 1.2
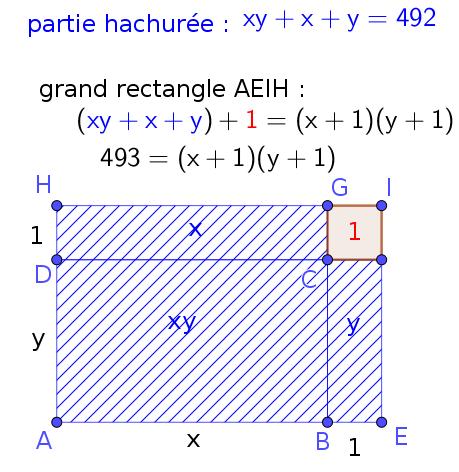
\((x+1)(y+1)=xy+x+y+1\) donc \(xy+x+y=492\) équivaut à \((x+1)(y+1)=493\) qui est « presque premier » (semi-premier) car égal à \(17\times29\) ;
on a donc \(x+1=1\) et \(y+1=493\) ou \(x+1=17\) et \(y+1=29\) (et symétriquement deux autres cas)
Ce qui donne comme solutions : \((0, 492)\), \((16, 28)\), \((28, 16)\) et \((492, 0)\), en ne considérant que des solutions non négatives, sinon, il y a en plus \((-2, 494)\), \((-18, -30)\), \((-494, -2)\) et \((-30, -18)\).
Complément : les nombres semi-premiers sont couramment utilisés en cryptologie en tant que clé publique pour le système RSA, parce qu’il est difficile de factoriser un grand nombre semi-premier.
En 1974, le message d’Arecibo a été envoyé sous la forme d’un signal radio vers un amas d’étoiles.
Il se composait de 1679 bits destinés à être interprétés comme une image binaire de 23 pixels sur 73. Le nombre \(1679 =23 \times 73\), a été choisi car il est semi-premier
et ne peut donc être arrangé en une image rectangulaire que de deux manières distinctes : 23 lignes et 73 colonnes ou 73 lignes et 23 colonnes.
Exercice 1.3
Notons \(N = 3n^2+n+1\)
Remarque : \(N\) est toujours impair car \(n\), \(n^2\) et \(3n^2\) ont la même parité donc \(3n^2+n\) est pair et \(3n^2+n+1\) est impair.
On en déduit que la somme des chiffres de \(N\) ne peut être égale à 1 ou 2 que dans les cas \(N=1\) ou \(N=10....01\)
Le cas \(N=1\) donne \(n=0\) ; sinon \(3n^2+n+1=10^k+1\) donne \(n(3n+1)=10^k\)
\(n(3n+1)=2^k.5^k\) ; or \(n\) et \(3n+1\) n’ont pas de diviseur commun, sinon ce serait un diviseur commun de (\(3n+1)-3n=1\).
Donc \(n = 2^k\) et \(3n+1=5^{k}\) (\(n<3n+1\) donc le cas inverse ne convient pas) ; on est donc ramené à l’équation \(3\times2^k+1=5^k\)
étude de cas particuliers avec un tableur
On remarque que pour \(k\geq2\) le premier membre est toujours strictement inférieur au deuxième, ce qu’on va démontrer :
\(3\times2^k+1<3\times2^k+2^k=4\times2^k\)
et il reste à démontrer que \(4\times2^k<5^k\)
c’est à dire (en divisant les deux membres par \(2^k\)) que \(4<(2,5)^k\),
ce qui est vrai dès que \(k\geq2\)
conclusion : étant donné que le tableau des exemples donné dans l’énoncé de l’exercice montre que la somme des chiffres de \(N\) peut être égale à 3 (pour \(n=8\)),
on en déduit que la somme des chiffres de \(3n^2+n+1\) est toujours supérieure ou égale à 3.
Qu’est-ce qu’un nombre ? 20231117

(Merci à Jean-Luc Mauriet pour ses commentaires graphiques)
Préliminaires
⚈ Utilisation du site : http://utl.manthano.fr
La navigation de page en page se fait en utilisant les flèches « gauche » et « droite » du clavier
Si la longueur d’une page excède la hauteur de l’écran, utiliser les flèches « haut » et « bas » du clavier
Certains liens ouvrent des pages externes que vous ne pouvez utiliser que si Geogebra et LibreOffice (ou Excel ?) sont installés sur votre ordinateur.
Le site est en construction et comporte pas mal de bugs : inadapté aux petits écrans, liens et menus qui ne fonctionnent pas, ... ; en cas de difficulté, rafraîchir la page.
⚈ Commentaires sur ce cours
Son caractère un peu « expérimental » ; d’où la nécessité de vos réactions.
⚈ Les « exercices »
Comment s’y prendre pour les résoudre ; correction de l’exerice 1.3
Exercices (série 2)
Exercice 2.1 : Que vaut le nombre décadique ...111 ?
Exercice 2.2 : (on ne considérera que des entiers strictement positifs)
a) Démontrer si on multiplie une somme de 2 carrés d’entiers par une autre somme de 2 carrés d’entiers, on obtient encore une somme de 2 carrés d’entiers.
b) Trouver 3 nombres premiers qui sont somme de 2 carrés d’entiers
c) Démontrer qu’il y a une infinité de nombres entiers qui sont somme de 2 carrés d’entiers
Solutions
Exercice 2.1
posons \(N=\ldots111\) ; \(N = 1 + 10 + 10^2 + 10^3 + \ldots\) ; alors \(10N=10+10^{2}+10^{3}+\ldots=N-1\) donc \(9N=-1\) d’où \(N=-\cfrac{1}{9}\).
On peut remarquer que si on pose les opérations (en admettant qu’elles se font de la façon habituelle) :
...111
× 9
__
= ...999
puis
...999
- 1
__
= ...000
ce qui donne \(9N+1=0\) soit \(N=-\cfrac{1}{9}\)
Exercice 2.2
partie a
\((a^2+b^2)(c^2+d^2)=a^2c^2+a^{2}d^{2}+b^{2}c^{2}+b^{2}d^{2}\)
\(=[a^{2}c^{2}+b^{2}d^{2}]+[a^{2}d^{2}+b^{2}c^{2}]\)
\(=[(ac+bd)^{2}-2acbd]+[(ad-bc)^{2}+2adbc]\)
\(= (ac+bd)^2+(ad-bc)^2-2acbd+2adbc\)
Les 2 derniers termes s’annulent, ce qui donne \((a^{2}+b^{2})(c^{2}+d^{2})=(ac+bd)^{2}+(bc-ad)^{2}\) égalité dans laquelle \(ac+bd\) et \(bc-ad\) sont des entiers si \(a\), \(b\), \(c\) et \(d\) sont des entiers
Complément : ce résultat peut s’interpréter géométriquement de la manière suivante
en remarquant que si \(\overrightarrow {U}\) et \(\overrightarrow{V}\) sont de vecteurs de coordonnées \((a,b)\) et \((c,d)\) dans un repère orthonormé,
alors \(a^{2}+b^{2}=||\overrightarrow{U}|| ^{2}\), \(b^2+c^2=||\overrightarrow{V}||^{2}\), \(ac+bd=\overrightarrow{U}.\overrightarrow{V}\) (produit scalaire) et \(ad-bc=\overrightarrow{U} \wedge \overrightarrow{V}\) (produit vectoriel)
donc l’égalité s’écrit : \(||\overrightarrow{U}||^{2}+||\overrightarrow{V}||^{2}=(\overrightarrow{U}.\overrightarrow{V})^{2}+||\overrightarrow{U} \wedge \overrightarrow{V}||^{2}\)
ce qui donne \(||\overrightarrow{U}||^{2}+||\overrightarrow{V}||^{2}=(||\overrightarrow{U}||^{2}.||\overrightarrow{V})||^{2}.cos^{2}(\overrightarrow{U},\overrightarrow{V}})+||\overrightarrow{U}||^{2}.||\overrightarrow{V}||^{2}.sin^{2}(\overrightarrow{U},\overrightarrow{V}})\), ce qui n’est finalement que la formule \(cos^{2}(\alpha)+sin^{2}(\alpha)=1\) !!!
partie b
par exemple \(5=2^2+1^{2}\), \(13=2^2+3^2\), \(17=1^{2}+4^{2}\)
complément (théorème de Fermat) : un nombre premier est somme de carrés si et seulement si il est de la forme \(4k+1\) avec \(k\) entier positif ; sa décomposition en somme de 2 carrés est unique.
partie c
si \(N\) est une somme de 2 carrés d’entiers, alors d’après la partie (a) \(N^{2} = N\times N\) est aussi une somme de carrés d’entiers, ainsi que \(N^{3}=N^{2}\times N\) ... et \(N^{k}\) récursivement pour tout entier \(k\)
Par exemple \(13=2^2+3^2\) donc \(13^3=2197=[(2^2+3^2)(2^2+3^2)](2^2+3^2)=[(2\times2+3\times3)^2+(2\times3-3\times2)^2](2^2+3^2)=13^2(2^2+3^2)=26^2+39^2\)
Remarque : on a aussi \(2197=9^2+46^2\)
Exercice 2.3
.jpg)
Pour que la preuve de la contradiction soit rigoureuse, il faut démontrer que \(BI\) est un entier.
Or \(\widehat{BIA}= 180°-\widehat{BAI}-\widehat{ABI}\) dans le triangle \(BIA\)
\(= 180 - \widehat{BDA}-\widehat{DAB}=\widehat{ABD}\) dans le triangle \(ADB\).
Donc \(BAI\) est isocèle ; d’où l’on déduit que \(AB=AI=DI\) puisque \(AID\) est isocèle.
Conclusion : \(BI=BD-DI=a-b\) donc c’est un entier (plus petit que \(a\)).
Distinguer le nombre de sa représentation

Si on pose la question à des « non spécialistes » on obtient en général la réponse : c’est une suite de chiffres (avec éventuellement une virgule).
On peut déjà dire que cette réponse n’aurait pas pu être donnée en Grèce antique où la notion de chiffre au sens actuel du terme n’existait pas. Il y a là confusion entre la nature du nombre et sa représentation.
Un autre problème posé par cette réponse est le fait de savoir si n’importe quelle suite de chiffres est un nombre déterminé de manière unique.
Exemple 1 (ambiguïté de la numération décimale)
\(9,999\ldots\) et \(10\) représentent le même nombre : en effet leur différence est égale à 0
autre explication : notons \(N = 9,999\ldots\) ; alors \(N = 9 + \cfrac{9}{10} + \cfrac{9}{100} + \ldots\) donc \(\cfrac{N}{10} = \cfrac{9}{10} + \cfrac{9}{100} + \ldots\)
soit \(\cfrac{N}{10} = N - 9\), ce qui donne \(N - \cfrac{N}{10} = 9\) soit \(\cfrac{9N}{10} = 9\) donc \(N = 10\).
Exemple 2 (nombres décadiques)

\(\ldots999,9\) est-il un nombre ?
si \(a=\ldots999,9\) alors \(=\cfrac{9}{10}+9+9\times 10+9\times 10^{2}+\ldots\)
\(10\times a=9+9\times 10+9\times 10^{2}+\ldots\) donc, par soustraction \(9\times a=-9/10\) donc \(a=-1/10\)
conclusion : \(\ldots999,9 = -0,1\)
Exemple 3
\(\ldots111 = ?\) (exercice 2.1)
Les nombres entiers
On peut penser que l’idée de nombre (entier) comme symbole (oral puis écrit) est survenue très tôt avec l’apparition du langage.
Un nombre entier positif, est alors ce qui sert à compter ; mais qu’est-ce que compter ?
Faisons un bond de quelques dizaines (centaines ?) de milliers d’années : un peu avant 1900 Cantor met en évidence que le comptage présuppose la capacité de mettre en correspondance deux collections. La construction de la théorie des ensembles va permettre une définition et une axiomatisation de la notion de nombre entier à partir de la théorie de ensembles.
Les débuts de l’arithmétique
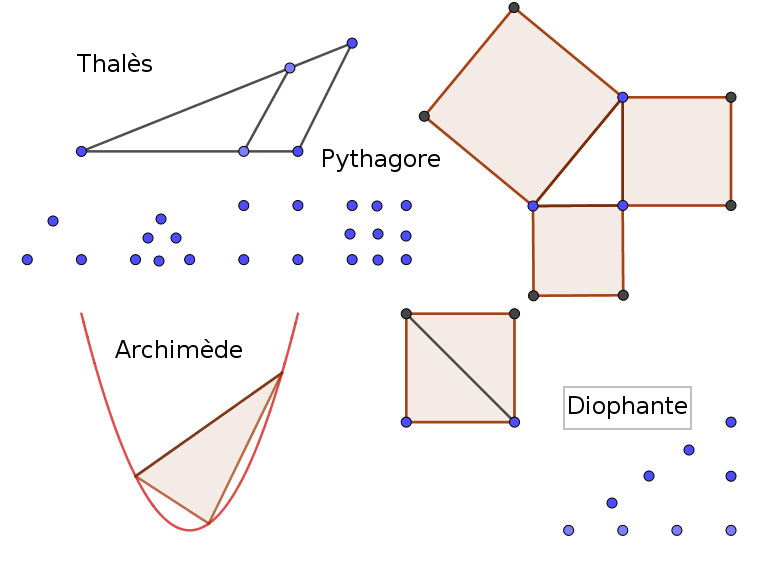
Conceptions pythagoriciennes
Pour Pythagore, Tout est nombre. Cette conviction lui est peut-être venue de l’astronomie. Les constellations se distinguent par leur nombre d’étoiles et par la disposition géométrique de celles-ci. En construisant diverses dispositions géométriques des nombres, les Pythagoriciens ont été les premiers à découvrir des propriétés abstraites des nombres.
En représentant les nombres par des points ou des cailloux, ils les ont classifié en nombres pairs et nombres impairs, et également par les formes géométriques selon lesquelles les points peuvent être disposés.
Les nombres figurés
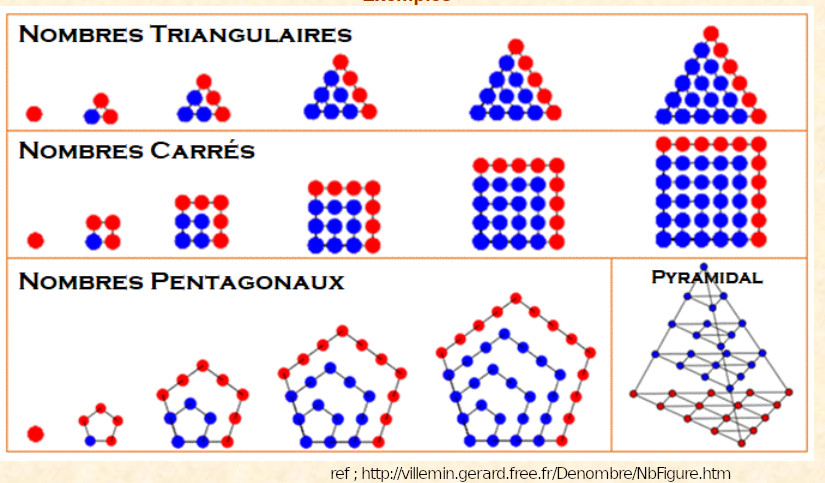
Pour les Pythagoriciens, multiplier des nombres correspond à calculer des aires de rectangles et les nombres carrés représentaient des aires de carrés.
Assemblages géométriques associés à certains nombres : premiers exemples de démonstrations ?
Les nombres carrés

Tout nombre impair est la différence de 2 carrés (correction de l’exercice 1.1) ; le gnomon est ici la représentation d’un nombre impair.
Tout carré est la somme de nombres impairs :
\(1 = 1^2 - 0^2\)
\(3 = 2^2 - 1^2\)
\(5 = 3^2 - 2^2\)
...
\(2n-1 = n^2-(n-1)^2\)
En additionnant membre à membre : \(1 + 3 + \ldots + (2n-1)=n^2\)
Les nombres triangulaires
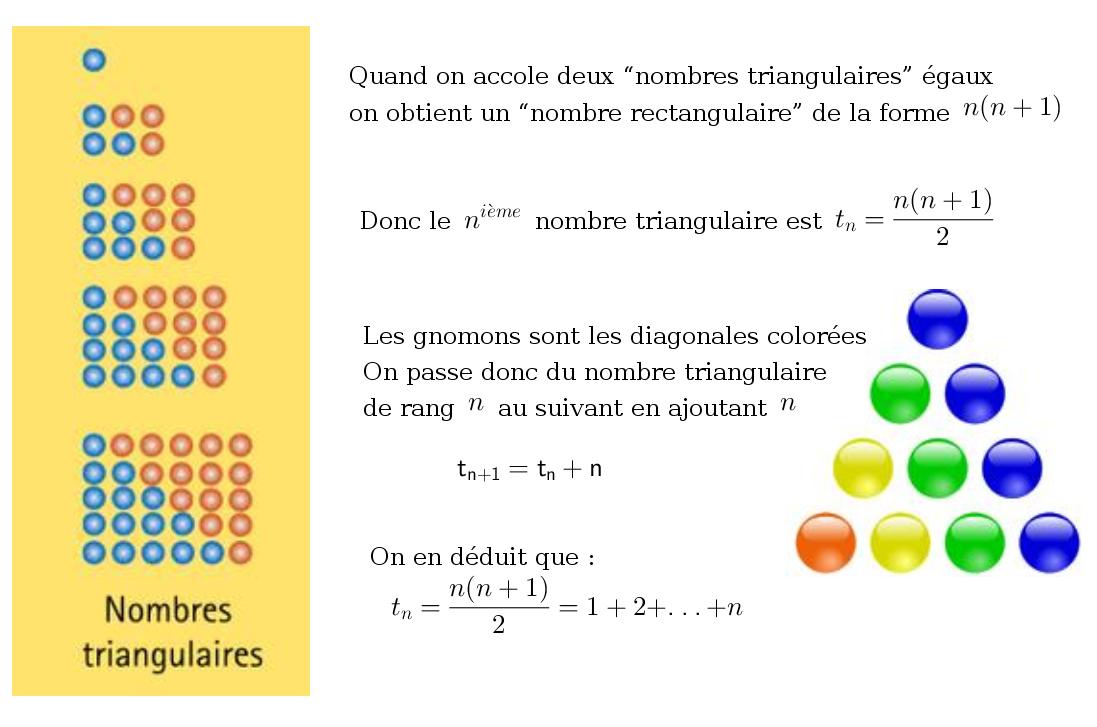
Le \(n^{ieme}\) nombre triangulaire est \(t_{n}=\cfrac{n(n+1)}{2}\)
Applications :
⚈ somme des \(n\) premiers nombres pairs (non nuls) : \(P = 2 + 4 + \ldots + 2n = 2(1 + 2 + \ldots + n) = n(n+1)\)
⚈ somme des \(n\) premiers nombres impairs : \(I=1+3+\ldots+(2n-1)=(\textcolor{red}{2}-1)+(\textcolor{red}{4}-1)+\ldots+(\textcolor{red}{2n}-1)=\textcolor{red}{P}-n\times1=n^{2}\)
⚈ \(n^2=t_n+t_{n-1}\)
Généralisation
Le n-ième nombre k-gonal est \(P^{(k)}_{n }=\cfrac{1}{2}n[(n-1)k-2(n-2)]\) (attention \((k)\) ne représente pas un exposant, mais indique le nombre de côtés du polygone)
Exemples
⚈ pour \(k=3\), on obtient les nombres triangulaires : \(\textcolor{red}{P^{(3)}_{n}}=\cfrac{1}{2}n[(n-1)\times3-2(n-2)]=\cfrac{1}{2}n[3n-3-2n+4]=\textcolor{red}{\cfrac{1}{2}n(n+1)}\)
⚈ pour \(k=4\), on obtient les nombres carrés : \(\textcolor{red}{P^{(4)}_{n}}=\cfrac{1}{2}n[(n-1)\times4-2(n-2)]=\cfrac{1}{2}n[4n-4-2n+4]=\cfrac{1}{2}n\times 2n=\textcolor{red}{n^{2}}\)
⚈ pour \(k=5\), on obtient les nombres pentagonaux : \(\textcolor{red}{P^{(5)}_{n}}=\cfrac{1}{2}n[(n-1)\times5-2(n-2)]=\cfrac{1}{2}n[5n-5-2n+4]=\textcolor{red}{\cfrac{1}{2}n(3n-1)}\)
La fonction génératrice des nombres k-gonaux est : \(g_k(x)=\cfrac{x[(k-3)x+1]}{(1-x)^3}\)
Correction de l’exercice 1.2
L’utilisation d’une figure géométrique pour résoudre l’équation \(xy+x+y=492\) pouvait permettre de trouver une factorisation. C’est ce type de méthodes qu’utilisaient les Grecs (qui ne disposaient pas du calcul algébrique) pour résoudre des problèmes ou effectuer des calculs de type algébrique.
Complément : séries (ou fonctions) génératrices
À partir du XVIIIème siècle, en particulier avec Euler (1748), l’utilisation de plus en plus courante des sommes formelles infinies (séries formelles) va conduire à associer une telle somme à une suite de nombres. Ceci va ensuite se développer en analyse combinatoire et en probabilités.
On associe à une suite \(u_0, u_1, u_2, \ldots, u_n, \ldots\) la série formelle \(U(X)=u_0+u_1X+u_2X^2+\ldots+u_nX^n+\ldots\) qu’on essaiera d’écrire sous une forme « finie » (forme close : sans pointillés)
Exemple 1 : suite constante \(u_n=1\) : \(U(X)=1+1.X+1.X^{2}+\ldots+1.X^{n}+\ldots\) dans laquelle on reconnaît \(U(X)=1+X+X^{2}+\ldots+X^{n}+\ldots=\cfrac{1}{1-X}\)
Exemple 2 : suite des entiers positifs : \(u_{n}=n\) pour \(n>0\)
On a \(u_{n+1}=u_{n}+1\)
donc \(U(X)=u_0+u_{1}X+u_{2}X^2+u_{3}X^3+\ldots\)
\(=u_0+(u_0+1)X+(u_1+1)X^2+(u_2+1)X^3+\ldots\)
\(= X+u_{1}X^2+X^2+u_{2}X^3+X^3+\ldots\) car \(u_0=0\)
\(= X+X^2+X^3+\ldots\)
\(+ X(u_{1}X+u_{2}X^2+u_{3}X^3+\ldots)\)
\(U(X)=1+2X+3X^{2}+4X^{3}+\ldots\)
\(=\textcolor{blue}{1}+(\textcolor{red}{1}+\textcolor{blue}{1})X+(\textcolor{red}{2}+\textcolor{blue}{1})X^2+(\textcolor{red}{3}+\textcolor{blue}{1})X^3+\ldots\)
\(=\textcolor{blue}{1+X+X^{2}+X^{3}+\ldots}\)
- \(\textcolor{red}{1}X+\textcolor{red}{2}X^{2}+\textcolor{red}{3}X^{3}+\ldots\)
\(U(X)=\textcolor{blue}{\cfrac{1}{1-X}}+X.U(X)\)
D’où : \((1-X)U(X)=\cfrac{1}{1-X}\) et \(U(X)=\cfrac{1}{(1-X)^2}\)
Exemple 3 : fonction génératrice des nombres triangulaires
Triangles pythagoriciens
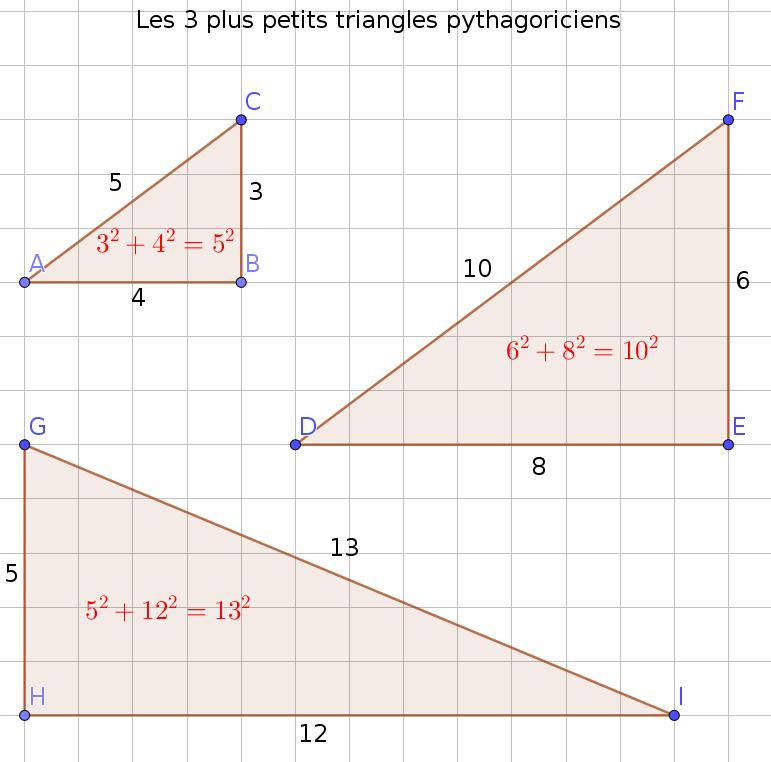
Un triangle pythagoricien est un triangle rectangle dont les côtés sont des nombres entiers (positifs).
Un triplet pythagoricien est un triplet \((a, b, c)\) de nombres entiers qui sont les côtés d’un triangle rectangle : \(a^{2}+b^{2}=c^{2}\)
La tablette Plimpton

On trouve des triplets pythagoriciens en Mésopotamie au IIème millénaire av. J.-C.
La deuxième colonne donne la valeur de a et la troisième colonne celle de c, le tout en notation sexagésimale écrite en cunéifome ; par exemple dans la première ligne on aurait :
| cunéiforme | décimal | sexagésimal moderne |
| 𒐕 𒐐𒐝 | 119 | 1:59 |
| 𒐖 𒐏𒐝 | 169 | 2:49 |
| 𒐖 (espace) | 120 | 2:0 |
On ne connaît ni la raison (construction d’un équivalent de nos tables trigonométriques ?) de la construction de ces tables, ni la méthode utilisée pour les obtenir (par essais et erreurs, à l’aide d’un algorithme...)
Pythagore, Euclide

Selon Proclus (Vème s.) Pythagore possédait une formule pour les triplets Pythagoriciens et on retrouve la trace de cette formule chez Platon puis dans le lemme 1 de la proposition 29 du livre X des Éléments d’Euclide qui démontre que si \(m\) et \(n\) sont deux entiers de même parité (avec \(n > m\)), alors \(\left(\cfrac{n^2-m^2}{2}, nm, \cfrac{n^2+m^2}{2}\right)\) est un triplet pythagoricien.
Avec \(n=3\) et \(m=1\) on trouve le triplet \((3, 4, 5)\), d’où une infinité \((3n, 4n, 5n)\), mais la formule ci-dessus ne donne pas tous les triplets pythagoriciens.
Interprétation en géométrie analytique
Chercher les triplets pythagoriciens, c’est chercher les solutions en nombres entiers de l’équation \(x^{2}+y^{2}=z^{2}\). Cette équation représente dans un repère un objet en dimension 3.
https://www.geogebra.org/classic/wrahq3nx (web)
Autre interprétation :
interprétation des solutions à l’aide de cercles concentriques dans le plan
Cas général 20231215
Le triplet \((a, b, c)\) est pythagoricien si et seulement s’il existe deux entiers m et n avec \(0 < m < n\) tels que \(\cfrac{a}{c}=\cfrac{n^2-m^2}{n^2+m^2}\) et \(\cfrac{b}{c}=\cfrac{2nm}{n^{2}+m^{2}}\)
triplets pythagoriciens et paramétrage du cercle unité
Les triplets pythagoriciens primitifs sont les triplets pythagoriciens \((a, b, c)\) tels que \(a\), \(b\), et \(c\) n’ont pas de diviseur commun.
L’un des deux nombres \(a\) ou \(b\) est alors impair (on peut supposer que c’est \(a\)) et on a alors :
\((a, b, c)\) est un triplet pythagoricien primitif (avec \(a\) impair) \(\Longleftrightarrow\) on peut écrire \(a=n^{2}-m^{2}\), \(b=2nm\) et \(c=n^{2}+m^{2}\) avec \(0 < m < n\) sans diviseur commun et de parités différentes.
exemples de triangles pythagoriciens
Complément
L’idée du paramétrage du cercle contient en germe beaucoup de notions mathématiques qui, étendues à des courbes plus compliquées que le cercle (courbes elliptiques - de degré 3 - par exemple) vont donner lieu à de nombreux résultats et développements à partir du XIXème siècle et jusqu’à maintenant dans plusieurs domaines des mathématiques :
- calcul des intégrales elliptiques et problème des périodes
- géométrie algébrique : théorie des groupes algébriques
- problèmes de géométrie diophantienne : théorème de Fermat-Wiles, conjectures de Weil, topologies de Grothendieck, ...
Tout ceci est au coeur du questionnement concernant les rapports entre le discret (arithmétique) et le continu (géométrie) dans les mathématiques actuelles.
paramétrage du cercle et structure de groupe algébrique
https://www.geogebra.org/m/enuekdz2 (web)
Extension : décompositions d’un entier en sommes de carrés
voir exercice 2.2
Les nombres premiers
Un nombre premier est un nombre qui a exactement deux diviseurs : 1 et lui-même (avec cette définition, 1 n’est pas un nombre premier).
Dans la représentation imagée de Pythagore, un nombre premier correspond à une nombre qui ne peut pas se mettre sous la forme d’un rectangle avec un côté supérieur à 1.
La décomposition en facteurs premiers
Les mathématiciens grecs de l’Antiquité avaient remarqué que les nombres premiers jouent un peu (en termes modernes) le rôle d’atomes (ou de « corps simples ») pour les nombres entiers.
Ils avaient démontré un certain nombre de faits importants :
⚈ tout nombre entier non premier possède un diviseur premier (Euclide - Éléments - Livre VII, proposition 31)
⚈ il existe une infinité de nombres premiers (Euclide - Éléments - Livre IX, proposition 20)
Ils utilisaient aussi couramment le fait que tout nombre entier peut se décomposer de manière unique (à l’ordre près) sous la forme d’un produit de nombres premiers : par exemple \(1500=2^2\times3\times5^3\)
problème concret de la découverte des facteurs premiers
L’une des méthodes de cryptographie couramment utilisée est basée sur le « petit » théorème de Fermat et la difficulté à décomposer un grand nombre entier en produit de facteurs premiers
cryptographie
voir : https://interstices.info/nombres-premiers-et-cryptologie-lalgorithme-rsa/
Explication de l’algorithme RSA
Je crée une clé publique de la manière suivante :
- je choisis deux nombres premiers : p = 5 et q = 17
- je calcule n = pq = 85 et k = (p - 1)(q - 1) = 64
- je choisis un entier e premier avec 64 : par exemple e = 15
- je choisis un entier d tel qu’il existe un entier relatif m vérifiant 15d + 64m = 1 (c’est à dire tel que 15d - 1 soit divisible par 64) en faisant des essais je trouve d = 47
- je rends publique ma clé (n, e) = (64, 15) ; ma clé secrète est d = 47
Si quelqu’un veut m’envoyer le message : A = 66 (il faut que A soit inférieur à n, sinon on le découpe)
Il calcule le reste de la division de Ae = 6615 par n = 64, ce qui donne B = 68
Il m’envoie B = 68
Je calcule le reste de la division de Bd = 681224 par n = 91, ce qui me donne 1
Elle calcule deux nombres premiers p et q, choisit e un nombre premier avec (p – 1)(q – 1) et d tel qu’il est défini dans le théorème, c’est-à-dire tel qu’il existe un nombre entier relatif m tel que :
e × d + m × (p – 1)(q – 1) = 1
Pour ce faire, elle peut utiliser un algorithme de calcul très connu depuis l’Antiquité (vers 300 ans avant Jésus-Christ) appelé algorithme d’Euclide.Elle calcule également n = p × q.
Alice rend publics les nombres n et e (par exemple en les publiant dans un annuaire, sur un site internet ou bien en les communicant directement à l’expéditeur, Bob). Elle conserve secrètement et bien cachés les nombres p, q et d, et peut même détruire p et q car ils ne serviront plus à personne.
Bob, qui veut transmettre une information secrète à Alice, transforme son information en un nombre entier A inférieur à n (ou en plusieurs nombres si nécessaire) avec un codage connu de tous.
Bob élève ensuite A à la puissance e, et prend le reste de la division du nombre qu’il a obtenu, Ae, par le nombre n que lui a également fourni Alice. Il envoie ce reste, que nous notons B, de façon non protégée.
Alice élève alors le nombre B que Bob vient de lui envoyer à la puissance d, qui est sa clé secrète, et obtient en prenant le reste de la division de Bd par n, par application du théorème du RSA, le message original que Bob lui a envoyé (car Bd ≡ (Ae)d [n] ≡ Aed[n] ≡ A [n] d’après le théorème du RSA).
Elle calcule deux nombres premiers p et q, choisit e un nombre premier avec (p – 1)(q – 1) et d tel qu’il est défini dans le théorème, c’est-à-dire tel qu’il existe un nombre entier relatif m tel que :
e × d + m × (p – 1)(q – 1) = 1
Pour ce faire, elle peut utiliser un algorithme de calcul très connu depuis l’Antiquité (vers 300 ans avant Jésus-Christ) appelé algorithme d’Euclide.Elle calcule également n = p × q.
Alice rend publics les nombres n et e (par exemple en les publiant dans un annuaire, sur un site internet ou bien en les communicant directement à l’expéditeur, Bob). Elle conserve secrètement et bien cachés les nombres p, q et d, et peut même détruire p et q car ils ne serviront plus à personne.
Bob, qui veut transmettre une information secrète à Alice, transforme son information en un nombre entier A inférieur à n (ou en plusieurs nombres si nécessaire) avec un codage connu de tous.
Bob élève ensuite A à la puissance e, et prend le reste de la division du nombre qu’il a obtenu, Ae, par le nombre n que lui a également fourni Alice. Il envoie ce reste, que nous notons B, de façon non protégée.
Alice élève alors le nombre B que Bob vient de lui envoyer à la puissance d, qui est sa clé secrète, et obtient en prenant le reste de la division de Bd par n, par application du théorème du RSA, le message original que Bob lui a envoyé (car Bd ≡ (Ae)d [n] ≡ Aed[n] ≡ A [n] d’après le théorème du RSA
Structure de l’ensemble des nombres premiers
Irrégularités de la suite des nombres premiers
Le mystère de l’organisation des nombres premiers : leur répartition « statistique » est connue, mais pas leur répartition réelle : on ne connaît pas de fonction \(f\) qui permettrait décrire le \(n^{\text{ième}}\) nombre premier \(p_{n}\) sous la forme \(p_{n}=f(n)\)
Théorème : étant donné un entier \(N \geq 2\), il existe toujours \(N - 1\) entiers consécutifs qui ne sont pas premiers.
Autrement dit : on peut trouver dans \(\mathbb{N}\) des intervalles arbitrairement grand ne contenant aucun nombre premier
En effet : \(N!=1\times 2\times 3\times 4\times \ldots \times (N-1)\times N\) est divisible par \(2, 3, 4, \ldots (N-1), N\)
donc : \(N!+2\) est divisible par \(2\), \(N!+3\) est divisible par \(3\), ... , \(N!+N\) est divisible par \(N\)
Aucun des \(N-1\) nombres ci-dessus n’est donc premier.
Exemples : (en prenant \(N = 5\)) aucun des nombres entiers de l’intervalle \(\left[ 5! + 2,5! + 5! \right]\) n’est premier, on a donc 4 nombres consécutifs non premiers \(122, 123, 124, 125\).
En prenant \(N = 50\), on obtient 49 entiers consécutifs non premiers,
de \(30414093201713378043612608166064768844377641568960512000000000002\)
à \(30414093201713378043612608166064768844377641568960512000000000050\)
Bonne année ! 20240212
Le crible d’Ératosthène

Ératosthène de Cyrène : IIIème siècle av. J.-C. ; directeur de la bibliothèque d’Alexandrie ; connu aussi pour avoir évalué la circonférence de la Terre.
voir : http://localhost:8888/lab/tree/inc/sagemath-jupyterlab/nombres%20premiers.ipynb
Le théorème de Hadamard - De La Vallée Poussin (1896)
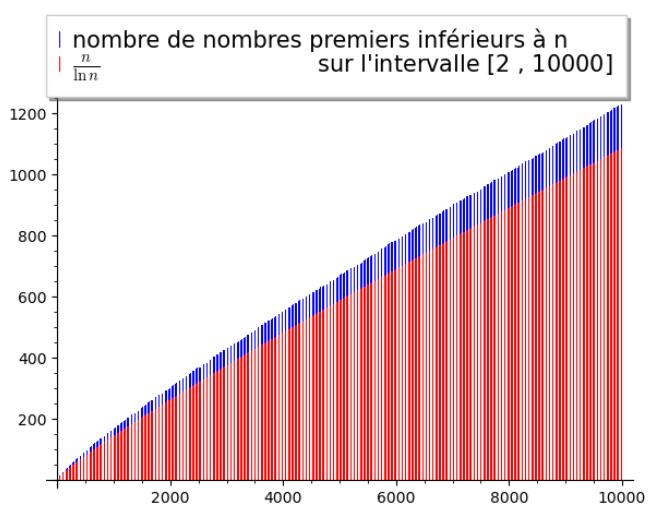
Ce théorème donne une répartition asymptotique des nombres premiers :
Le nombre \(\pi(x)\) de nombres premiers inférieurs à \(x\) est équivalent à \(\cfrac{x}{\ln x}\) quand \(x\) tend vers l’infini.
Ceci équivaut au fait que, quand \(n\) tend vers l’infini le \(n^{\text{ième}}\) nombre premier, noté \(p_{n}\), est approximativement \(n.\ln n\).
Depuis, beaucoup de travaux ont porté sur l’estimation de l’erreur commise en utilisant ces formules et ont montré les liens existant entre ces problèmes et le conjecture de Riemann concernant la fonction \(\zeta\)
Ce domaine de l’arithmétique est lié à l’analyse complexe.
La conjecture des nombres premiers jumeaux
Conjecture : il existe une infinité de couples de nombres entiers de la forme \((p, p + 2)\) avec \(p\) et \(p + 2\) tous les deux premiers.
Les plus petits nombres premiers jumeaux sont \((3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43)\)
Les nombres premiers jumeaux les plus grands connus actuellement sont \(2 996 863 034 895 \times 2^{1 290 000} - 1\) et \(2 996 863 034 895 \times2^{1290000} + 1\) ; les deux nombres possèdent 388342 chiffres.
En 2014, dans le cadre du projet Polymath (Terence Tao, Timothy Gowers), on a démontré qu’il existe une infinité de couples \((p, q)\) de nombres premiers tels que \(q - p \leq 246\)
La conjecture de Goldbach (1742)
Conjecture : tout nombre entier pair est la somme de deux nombres premiers
Exemples : \(4 = 2 + 2 ; 6 = 3 + 3 ; 8 = 3 + 5 ; 10 = 3 + 7 = 5 + 5 ; ... ; 50 = 3 + 47 = 7 + 43 = 13 + 37 = 19 + 31\) ; en 2013 on a vérifié le résultat jusqu’à \(n = 4.10^{18}\)
En 1995, Olivier Ramaré a démontré que tout nombre entier pair est la somme d’au plus 6 nombres premiers.
Des entiers aux fractions
La division \(\cfrac{a}{b} = c\) si \(b \times c = a\) de deux nombres entiers ne donne pas toujours une nombre entier. Géométriquement les fractions interviennent dans le théorème de Thalès.
L’introduction des fractions comme quotients \(\cfrac{a}{b}\) avec \(a\) et \(b\) entiers et \(b\neq0\) correspond à la nécessité de pouvoir faire des divisions entre entiers. Cependant, par ce processus, « on perd l’unicité » de l’écriture : \(\cfrac{a}{b}\) est égal à \(\cfrac{c}{d}\) lorsque \(a\times d=b\times c\).
Une fraction (ou nombre rationnel) peut être définie comme un couple \((a, b)\) de nombres entiers avec \(b\) non nul. \(\cfrac{a}{b}\) est l’ensemble des couples \((x, y)\) tels que \(a\times y=b\times x\)
On perd l’unicité de l’écriture.
Remarque : le concept de fraction permet de donner un sens à la division lorqu’elle est « impossible » dans l’ensemble des nombres entiers ; on peut remarquer que la nécessité d’étendre le champ de la division est apparue bien avant la nécessité d’étendre le champ de la soustraction, ce qui donnera les nombres négatifs.
Écriture décimale
L’écriture décimale, qui se répand en Europe à partir du XIIème siècle conduit « presque » à une écriture unique d’une fraction, sauf dans les cas comme 0,999... = 1 par exemple.
On s’aperçoit alors que l’écriture décimale d’une fraction peut être
- finie, comme \(\cfrac{2}{25}=0,08\)
- infinie périodique comme \(\cfrac{1}{3}=0,333\ldots\) où la période est 3 ou bien comme \(\cfrac{3}{14}=0,2\textcolor{red}{142057}\textcolor{green}{142057}\dots\) où la période est 142057.
On en déduit par exemple que la constante de Champernowne \(C = 0,1234567891011121314\ldots\) (les décimales sont obtenues en écrivant côte à côte les nombres entiers) n’est pas un nombre rationnel.
Exercice 3.1 :
a) quelle est le nombre maximal de chiffres de la période d’une fraction ?
b) quelle est la fraction dont l’écriture décimale est \(0,12\textcolor{red}{3456789}\textcolor{green}{3456789}\ldots\) (la période est 3456789) ?
Corrigé :
a) Quand on pose la division euclidienne \(\cfrac{a}{b}\) les restes successifs sont inférieurs à l’entier \(b\) ; donc il y a au maximum \(b-1\) restes non nuls différents ; au bout d’au maximum \(b\) étapes on va retomber sur un reste déjà obtenu précédemment ; la longueur de la période est donc \(b\) au maximum.
b) posons \(a = 0,123456789\ldots\)
\(100\times a=12,3456789\ldots\)
\(100\times a-12=0,3456789\ldots\)
\(10^{7}\times(100\times a - 12)=3456789+(100\times a -12)\)
\((10^7-1)\times(100\times a - 12)=3456789\)
$a\(100\times a-12=\cfrac{3456789}{10^{7}-1}\)
finalement \(a=\cfrac{\cfrac{3456789}{10^{7}-1}+12}{100}=\cfrac{41152259}{333333300}\)
Les irrationnels
Corrigé de l’exercice sur le nombre d’or
Exercice 2.3 : Ci-dessous on donne une démonstration du fait que le rapport de la diagonale d’un pentagone à son côté n’est pas une fraction ;
à la fin de la preuve la contradiction comporte une imprécision : il manque un argument pour que ce soit rigoureux ; lequel ?
Essayer de compléter la fin de la preuve pour avoir un raisonnement rigoureux.
.jpg)
Solution
Pour que la preuve de la contradiction soit rigoureuse, il faut démontrer que \(BI\) est un entier.
Or \(\widehat{BIA}= 180°-\widehat{BAI}-\widehat{ABI}\) dans le triangle \(BIA\)
\(= 180 - \widehat{BDA}-\widehat{DAB}=\widehat{ABD}\) dans le triangle \(ADB\).
Donc \(BAI\) est isocèle ; d’où l’on déduit que \(AB=AI=DI\) puisque \(AID\) est isocèle.
Conclusion : \(BI=BD-DI=a-b\) donc c’est un entier (plus petit que \(a\)).
\(\sqrt{2}\)
Les mathématiciens de la Grèce Antique on démontré que la diagonale du carré est incommensurable avec son côté, c’est à dire que \(\sqrt{2}\) est irrationnel.
On considère souvent que cet exemple, ou celui du nombre d’or, ont représenté un « obstacle épistémologique » important dans leur représentation mathématique du monde.
Ce n’est qu’au XXème siècle qu’on parviendra à construire un statut rigoureux pour les nombres irrationnels.
L’ensemble des irrationnels \(\mathbb{R}-\mathbb{Q}\)
Quand on additionne, soustrait, multiplie, divise ou élève à une puissance des nombres irrationnels, obtient-on des nombres irrationnels ?
\(\sqrt{2}\times\sqrt{3}=\sqrt{6}\) ; \(\sqrt{2}\times\sqrt{8}=4\) ;
\((\sqrt{5} - 1)\times(\sqrt{5} + 1)=4\)
puissances de racine de 2
Théorème : il existe des nombres irrationnels \(a\) et \(b\) tel que \(a^{b}\) soit rationnel
démonstration : prenons \(a =\sqrt{2}\) et \(b=\sqrt{2}\) alors :
- supposons que \(\sqrt{2}^{\sqrt{2}}\) est rationnel, alors le théorème est démontré (avec \(a = \sqrt{2}\) et \(b=\sqrt{2}\))
- sinon \(\sqrt{2}^{\sqrt{2}}\) est donc irrationnel mais \(\left(\sqrt{2}^{\sqrt{2}}\right)^{\sqrt{2}}=\sqrt{2}^{\sqrt{2}\times\sqrt{2}}=\sqrt{2}^{2}=2\) qui est rationnel donc le théorème est démontré (avec \(a=\sqrt{2}^{\sqrt{2}}\) et \(b=\sqrt{2}\))
Remarques :
- ceci ne permet pas de dire que \(\sqrt{2}^{\sqrt{2}}\) est rationnel ou irrationnel ; ce n’est qu’en 1934 que Gelfond et Schneider on démontré que c’était un irrationnel (et même un transcendant)
- si on utilise des nombres transcendants, c’est évident : \(e^{\ln 2}=2\) ; mais on ne sait pas par exemple si \(2^e\), \(\pi + e\), \(\pi^e\) et \(\pi^\sqrt{2}\) sont rationnels.
Représentation décimale des fractions
L’écriture décimale des nombres, apparue en Europe Occidentale entre le Xème et le XIIIème siècle, permet de caractériser les nombres rationnels : ce sont les nombres qui ont une écriture décimale périodique.
Fractions continues
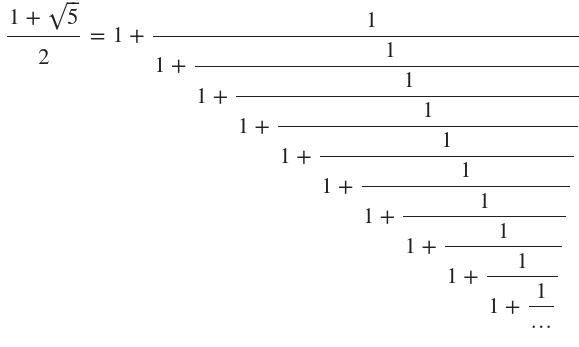
L’écriture fractionnaire, en étendant à l’infini son champ d’application, peut conduire à la création de nombres irrationnels
voir : http://localhost:8889/lab/tree/inc/sagemath-jupyterlab/fractions%20continues.ipynb
On peut démontrer que :
- un rationnel a un développement en fraction continue fini
- un irrationnel a un développement en fraction continue infinie périodique si et seulement si il est solution d’une équation du second degré à coefficients entiers ou rationnels.
Les nombres transcendants
Parmi les irrationnels on peut distinguer deux sous-ensembles
- ceux qui sont solutions d’une équation polynomiale à coefficients rationnels : ce sont les nombres algébriques
- les nombres transcendants : \(e\), \(\pi\), ...
Kronecker

Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.
Dieu a fait les nombres entiers, le reste est l’œuvre de l’homme
Comment mathématiser cette « œuvre de l’homme », c’est à dire ce processus de construction des nombres à partir des entiers (ou à partir des fractions) ?
Quelques exemples
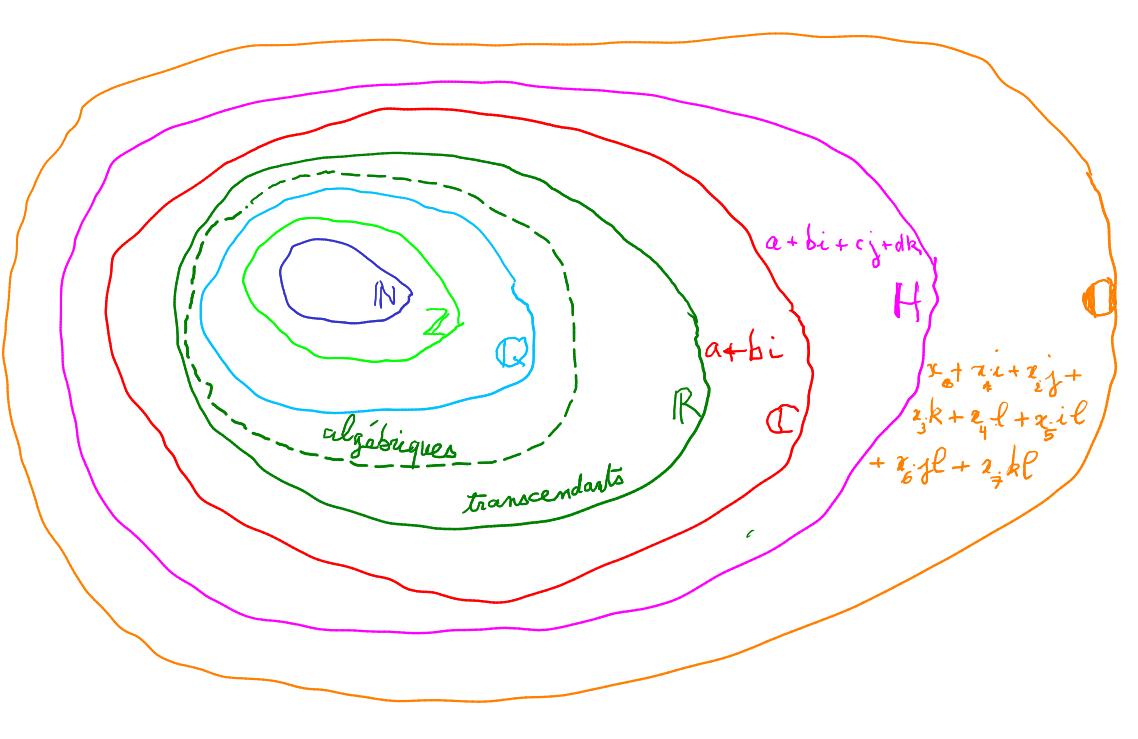
- les nombres obtenus à partir d’un passage à la limite dans les sommes infinies ou les fractions continues : on obtient ainsi les racines, \(e\), \(\pi\)
- les nombres obtenus en ajoutant un irrationnel algébrique (par exemple \(\sqrt{2}\)) à l’ensemble \(\mathbb{Q}\) des fractions.
On obtient un ensemble nommé \(\mathbb{Q}(\sqrt{2})\) qui possède les mêmes propriétés algébriques que \(\mathbb{Q}\) relativement à l’addition et à la multiplication. Dans le cadre de la théorie algébrique des nombres, motivé par exemple par la recherche d’une démonstration du théorème de Fermat, et plus généralement par la recherche des solutions des équations algébriques, les mathématiciens du XVIIIème au XXème siècle vont étudier les propriétés dans ces ensembles de nombres : analogie avec les nombres entiers et les nombres premiers, problèmes de divisibilité, ... - plus généralement les nombres obtenus en ajoutant à l’ensemble \(\mathbb{R}\) les solutions de l’équation \(x^{2}=-1\) : on obtient l’ensemble \(\mathbb{C}\) des nombres complexes, qui lui même sera étendu en l’ensemble des quaternions puis en l’ensemble des octonions au XIXème siècle.
Les structures algébriques
On va s’apercevoir aussi qu’il existe d’autres ensembles dont les éléments « se comportent comme des nombres » mais qui ne sont pas obtenus par extension de \(\mathbb{Q}\) et \(\mathbb{R}\) : les corps finis.
Petit à petit va s’imposer l’idée selon laquelle les nombres sont définis dans des ensembles munis d’opérations algébriques qui prolongent l’addition et la multiplication. On va s’intéresser aux « structures » (groupe, anneau, corps, ...) qui définissent les règles opératoires.
Correction des exercices 20240126

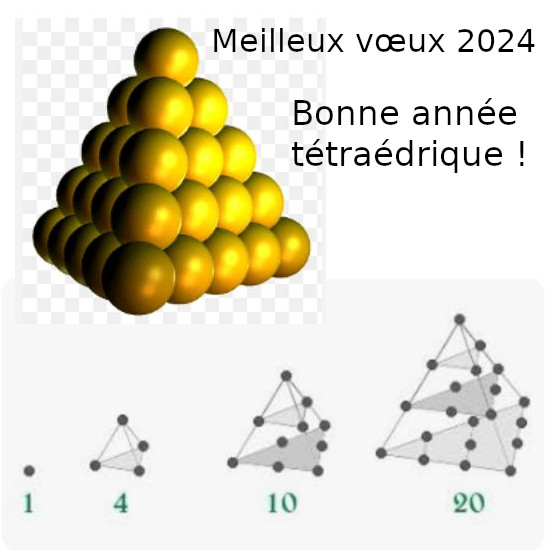
Exercice 4.1
a) Démontrer que le \(n^{ieme}\) nombre tétraédrique s’écrit sous la forme \(\cfrac{n(n+1)(n+2)}{6}\) (on pourra utiliser le fait que la somme des \(n\) premiers entiers est \(\cfrac{n(n+1)}{2}\) et que la somme des \(n\) premiers carrés est \(\cfrac{n(n+1)(2n+1)}{6}\))
b) Déterminer les nombres triangulaires consécutifs tels que \(1 + 3 + 6 + 10 + \ldots = 2024\)
c) Quelle était la précédente année tétraédrique ?
d) Quelle sera le prochaine année tétraédrique ?
Exercice 4.2
Écrire le développement en fraction continue de \(\sqrt{5}\)
Correction des exercices 4.1 et 4.2
Exercice 4.1
a) \(T_n=\cfrac{1\times2}{2}+\cfrac{2\times3}{2}+\cfrac{3\times 4}{2}+\dots+\cfrac{i(i+1)}{2}+\ldots+\cfrac{n(n+1)}{2}\) donc
\(2T_n=1\times(1+1)+2(2+1)+3(3+1)+...+n(n+1)=1^2+2^2+\ldots+n^2 + 1+2+...+n\)
\(=\cfrac{n(n+1)(2n+1)}{6}+\cfrac{n(n+1)}{2}=\cfrac{n(n+1)(2n+1)}{6} +3\times\cfrac{n(n+1)}{6}\)
\(=\cfrac{n(n+1)(2n+1+3)}{6}=\cfrac{n(n+1)(2n+4)}{6}=\cfrac{n(n+1)(n+2)}{3}\)
donc \(T_n=\cfrac{n(n+1)(n+2)}{6}\)
b) Quel est le rang \(n\) de l’année tétraédrique 2024 ?
\(2024=\cfrac{n(n+1)(n+2)}{6}\) donne \(12144 =n(n+1)(n+2)\) ; or \(12144=22\times23\times24\) (pour trouver cette décomposition on peut calculer \(\sqrt[3]{12144}\simeq 22,98\))
donc \(n = 22\)
L’année tétraédrique précédente sera obtenue en prenant \(n=21\) ce qui donne 1771 ;
la suivante, pour \(n=23\) sera 2300.
Exercice 4.2
\(x=\sqrt{5}\) est solution de l’équation \(x^2-5=0\) soit \(x^2-4=1\) c’est à dire \((x-2)(x+2)=1\)
Ce qui donne \(x-2=\cfrac{1}{2+x}\) donc \(x=2+\cfrac{1}{2+x}=2+\cfrac{1}{2+2+\cfrac{1}{2+x}}=2+\cfrac{1}{4+\cfrac{1}{2+x}}=2+\cfrac{1}{4+\cfrac{1}{4+\cfrac{1}{4+\ldots}}}\)
Intermède : logarithmes et exponentielles
Les tables de logarithmes
En 1614, pour faciliter les calculs, en particulier en astronomie, Neper (John Napier) invente la notion de logarithme, dont l’objectif est de transformer une multiplication en addition.
Cela se présente comme des tables de correspondances entre deux séries de valeurs \(a\) et \(L(a)\) telles que \(L(a\times b)=L(a)+L(b)\)
En choisissant 10 comme valeur telle que \(L(10)=1\), Briggs invente en 1624 les logarithmes décimaux (qu’on notera \(\log\) : \(\log a=b\) si \(10^{b}=a\)
Remarque : avec les logarithmes s’introduisent de nouveaux nombres irrationnels ; démontrons par exemple que le logarithme décimal de 2 est irrationnel :
logarithmes décimaux
logarithme décimaux (version en ligne)
supposons \(\log 2=\cfrac{m}{n}\) fraction irréductible ;
cela signifie que \(10^\frac{m}{n}=2\) soit \(\left(10^m\right)^\frac{1}{n}=\sqrt[n]{10^m}=2\) c’est à dire \(2^n=10^m\) ;
si \(m=0\) cela donne \(2^n=1\) donc \(n=0\) et la fraction \(\cfrac{n}{m}\) n’est pas définie ;
sinon \(10^m\) est divisible par 5, ce qui aboutit à une contradiction car \(2^n\) n’est pas divisible par 5.
Les fonctions logarithmes
Rappel : au début du XVIIème siècle, en utilisant - entre autres - la méthode des indivisibles de Cavalieri, les mathématiciens (Fermat par exemple, en 1636) ont réussi à calculer l’aire sous les courbes d’équations \(y=x^k\) pour toute fraction \(k\) différente de -1 ; ils obtiennent la formule \(\displaystyle\int_{0}^{t}{x^k}dx=\cfrac{x^{k+1}}{k+1}\) pour \(k\geq0\) et \(\displaystyle\int_{1}^{t}{x^k}dx=\cfrac{x^{k+1}}{k+1}-\cfrac{1}{k+1}\) pour \(k<0\) avec \(k\neq -1\)
Mais ils ne trouvent pas la solution lorsque \(k=-1\).
En 1647, Grégoire de Saint-Vincent démontre que la fonction \(F\) qui donne l’aire sous la courbe d’équation \(y=\cfrac{1}{x}\) entre 1 et \(t\) vérifie la propriété \(F(a\times b)=F(a)+F(b)\)
Mais c’est son élève Sarasa qui fait le lien en 1649 avec le travail de Neper et se rend compte que \(F\) est un logarithme.
Avec les notations de Leibniz, on peut écrire \(\ln t = \displaystyle {\int_{1}^{t}\frac{1}{x}dx}\) ce qui peut se lire : surface entre 1 et \(t\) sous la fonction \(\cfrac{1}{x}\)
logarithme néperien
logarithme népérien (version en ligne)
Résumé 20240209
On constate que la construction des fonctions logarithmes résulte d’un processus complexe mettant en oeuvre des problèmes provenant de différents domaines :
- la construction de « tables de logarithmes » permettant de simplifier les calculs (en particulier en astronomie) en remplaçant les multiplications par des additions
- la tentative de généralisation à la fonction \(\cfrac{1}{x}\) des formules de calcul d’aires du type \(\displaystyle\int x^k=\cfrac{x^{k+1}}{k+1}\) pour \(k\neq -1\) ; on obtient \(\displaystyle\int_{1}^{t}{\cfrac{1}{x}dx=L(t)\) où \(L\) est une fonction qui possède les propriétés caractéristiques des logarithmes : \(L(a\times b)=L(a)+L(b)\) et \(L(1)=0\). On notera \(L=\ln\) et il existe un nombre \(e\) tel que \(\ln e =1\)
- ce nombre \(e\) apparaît dans la détermination du taux d’intérêt (dit continu) équivalant à un taux d’intérêt annuel de 100% mais calculé continûment, c’est à dire à chaque instant. On montre que ce nombre \(e\) est donné par la formule \(e=\lim\limits_{n\to \infty }\left(1+\cfrac{1}{n}\right)^{n}\), ce qui permet d’en calculer des valeurs approchées.
Plus généralement, si t est le taux d’intérêt (en prenant t = 1 pour 100%), le taux d’intérêt continu serait \(e^t=\lim\limits_{n\to \infty }\left(1+\cfrac{t}{n}\right)^{n}\)
On voit donc apparaître ici une relation entre le nombre \(e\) relatif à une éventuelle réciproque de la fonction \(\ln\) (puisque \(e\) est le nombre tel que \(\ln e = 1\)) et une « fonction » exponentielle.
logarithmes (synthèse)
Les calculs d’intérêts

En 1690 Jacques Bernoulli découvre une constante qu’on va nommer provisoirement \(E\) par l’étude d’une question concernant les intérêts composés et qui est égale à \(\lim\limits_{n\to \infty }\left(1+{\cfrac {1}{n}}\right)^{n}}\).
Soit comme exemple, un compte qui a pour valeur initiale \(S\) (en euros) et rapporte 100% d’intérêt par an ; au bout d’un an, le compte a pour valeur \(2.S\).
Mais si l’intérêt est composé tous les 6 mois, \(S\) est multiplié par 1,5 chaque semestre, ce qui donne \(S \times 1.5^2 = 2,25\times S\)
Si l’intérêt est composé chaque trimestre : \(S \times1,25^4 = 2,441 4\ldots \times S\)
Et s’il est mensuel, \(S \times \left(1+\cfrac{1}{12}\right)^{12}= 2,613 035\ldots \times S\).
Bernoulli a remarqué que cette suite tend vers une limite (le taux d’intérêt effectif) lorsque les intervalles deviennent de plus en plus petits. Pour un intérêt composé chaque semaine, on trouve \(2,692 597\ldots \times S\), pour un intérêt composé chaque jour, on trouve \(2,714567 \ldots \times S\)
Si \(n\) est le nombre d’intervalles de composition, avec un taux d’intérêt égal à \(\cfrac{1}{n}\) (soit \(\cfrac{100~\%}{n}\)) pour chaque intervalle, la limite lorsque \(n\) devient grand, est le nombre d’Euler qui par la suite a été noté \(e\). Pour des intérêts composés continûment, la valeur du compte atteindra \(2,718 281 8\ldots \times S\).
Plus généralement, un compte dont la valeur initiale est S, et un taux \(t\), aura au bout d’un an la valeur finale \(e^t\times S\) euros lorsqu’on découpe l’année en une infinité de périodes de composition infiniment courtes.
Autrement dit : \(E^t=\lim\limits_{n\to \infty }\left(1+\cfrac{t}{n}\right)^{n}\)
Utilisation des limites et des sommes (séries) infinies
Problèmes posés par les séries infinies
Au milieu du XVIIème siècle apparaissent les techniques de développement en séries infinies, ce qui revient à utiliser, en sus des opérations « de base » (addition, soustraction, multiplication, division, racines) une nouvelle opération : les sommes infinies.
Les mathématiciens ne se soucient pas trop à cette époque de la validité de cette opération, c’est à dire des problèmes de convergence : une somme infinie de nombres est-elle encore un nombre, peut-on appliquer les opérations de base aux sommes infinies ? On dirait actuellement qu’ils raisonnent dans l’anneau de séries formelles \(\mathbb{R}[[X]]\).
En effet, les expressions du type : \(\cfrac{1}{1-x}=1+x+x^{2}+x^{3}+x^{4}+x^{5}+\ldots\) se démontrent formellement par un calcul algébrique sur des sommes infinies ; ont-elles un sens lorsqu’on remplace \(x\) par un nombre quelconque ? On démontrera plus tard que ceci n’a de sens que si \(x\) est compris entre -1 et 1 ; mais pour cela il faudra construire la notion de convergence.
exemples
exemples (version en ligne)
Question : comment expliquer les contradictions rencontrées dans certains cas, alors que dans d’autres cas on trouve des résultats cohérents (notion de rayon de convergence)
Approximations
Calcul de \(\ln 2\)
En 1657, Mercator puis Wallis utilisent
\(\displaystyle{\ln(1+t)=\int_{0}^{t}\frac{1}{1+x}dx=\int_{0}^{t}\left(1-x+x^{2}-x^{3}+\ldots\right)dt=\int_{0}^{t}1.dx-\int_{0}^{t}x.dx+\int_{0}^{t}x^{2}.dx-\int_{0}^{t}x^{3}.dx+\ldots=t-\frac{t^{2}}{2}+\frac{t^{3}}{3}-\frac{t^{4}}{4}+\ldots}\)
pour obtenir \(\ln 2=1-\cfrac{1}{2}+\cfrac{1}{3}-\cfrac{1}{4}+\ldots\) mais la convergence est très lente.
Newton va améliorer la convergence.
approximations de ln 2
approximations de ln 2 (version en ligne)
La fonction exponentielle 20240209
Introduction
La définition de la fonction \(\ln\) montre qu’il existe un entier \(e\) tel que \(\ln e = 1\)
Par ailleurs, et indépendamment, Jacques Bernoulli met en évidence, dans le calcul des « intérêts composés continus »,
- qu’un taux d’intérêt annuel égal à 100%, si on calcule les intérêts « continûment », c’est à dire à chaque instant, multiplie le capital par une constante, qu’on va provisoirement nommée \(E\), égale à \(E=\lim\limits_{n\to \infty}\left(1+\cfrac {1}{n}\right)^{n}\)
- et plus généralement un taux d’intérêt annuel \(t\) (avec \(t=1\) pour 100%), multiplie la capital par \(E^t=\lim\limits_{n\to \infty }\left(1+\cfrac{t}{n}\right)^{n}\)
Remarques
Ces formules ne permettent pas de calculer \(E\) de manière efficace :
\(n\) 10 100 1000 10000 \(E\) 2,5937 2,7048 2,7169 2,7181
alors que \(E=2,7182\ldots\)
- La formule donnant \(E^{t}\) suggère l’existence d’une « fonction exponentielle »
Identification de \(E\) avec \(e\)
\(E=\lim\limits_{n\to \infty}\left(1+\cfrac {1}{n}\right)^{n}\) donc \(\ln E \simeq n.\ln \left(1+\cfrac{1}{n}\right)\) pour \(n\) grand,
soit \(\ln E \simeq n\left(\cfrac{1}{n}-\cfrac{\cfrac{1}{n^{2}}}{2}+\cfrac{\cfrac{1}{n^{3}}}{3}-\ldots\right)\simeq 1-\cfrac{\cfrac{1}{n}}{2}+\cfrac{\cfrac{1}{n^{2}}}{3}-\ldots\)
avec tous les termes où \(n\) apparaît qui s’annulent quand \(n\) tend vers l’infini.
Donc \(\ln E =1\), c’est à dire \(E=e\).
Développement en série de la fonction exponentielle
La formule \(e^x=\lim\limits_{n\to \infty }\left(1+\cfrac{x}{n}\right)^{n}\) conduit peu à peu à considérer l’exponentielle comme une fonction.
Newton et Euler, utilisant le développement du binôme de Newton \((1+t)^k=1+kt+\cfrac{k(k-1)}{2!}t^2+\cfrac{k(k-1)(k-2)}{3!}t^3+\ldots\)
obtiennent, en posant \(t=\cfrac{x}{n}\) et \(k=n\) :
\(e^x=1+x+\cfrac{n(n-1)}{2!}\left(\cfrac{x}{n}\right)^2+\cfrac{n(n-1)(n-2)}{3!}\left(\cfrac{x}{n}\right)^3+\ldots\) quand \(n\) tend vers l’infini.
En remarquant que quand \(n\) tend vers l’infini, dans chacun des termes de la somme l’expression \(\cfrac{n(n-1)(n-2)\ldots(n-j)}{n^{j+1}}\) tend vers 1, ils trouvent :
\(e^x=1+x+\cfrac{x^2}{2!}+\cfrac{x^3}{3!}+\ldots\)
Ceci va avoir deux conséquences :
- on va pouvoir calculer des valeurs approchées de \(e\) plus efficacement
- on va démontrer que la fonction exponentielle transforme les sommes en produits : c’est la réciproque de la fonction logarithme
Calcul de valeurs approchées de \(e\)
\(e^x=1+x+\cfrac{x^2}{2!}+\cfrac{x^3}{3!}+\ldots\)
En prenant \(x=1\) cette formule permet de calculer \(e\) beaucoup plus efficacement.
| \(n\) | 5 | 10 | 15 |
| \(e\) | 2.70833333333333 | 2.71828152557319 | 2.71828182845823 |
alors que \(e = 2,7182845904523536028747\ldots\)
Développement de \(e\) en fraction continue
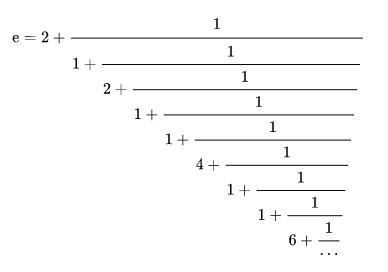
Euler obtient en 1737 le dévelppement de \(e\) en fraction continue. Ceci fournit une méthode de calcul encore plus efficace que le développement en série.
Le fait que ce développement soit infini prouve que \(e\) n’est pas un nombre rationnel.
Le fait qu’il ne soit pas périodique montre qu’il n’est pas solution d’une équation du second degré.
Ce n’est que 150 ans plus tard, en 1874, que Charles Hermite démontrera que c’est un nombre transcendant.
Fonction réciproque du logarithme népérien
Le développement en série de l’exponentielle permet de démontrer que la fonction exponentielle transforme les sommes en produits ; c’est la fonction réciproque du logarithme népérien.
problème des sous-tangentes
problème des sous-tangentes (version en ligne)
fonctions réciproques _ logarithme népérien et exponentielle
fonctions réciproques _ logarithme neperien et exponentielle (version en ligne)
Conclusion
On constate à nouveau que, comme pour le logarithme, la construction de la notion d’exponentielle résulte d’un processus complexe mettant en oeuvre des problèmes provenant de différents domaines :
On a constaté aussi que l’exponentielle peut être définie de plusieurs manières :
- \(e^{x}=\lim\limits_{n\to \infty }\left(1+\cfrac{x}{n}\right)^{n}\) dans le calcul du « taux d’intérêt continu »
- \(e^{x}=1+\cfrac{x}{1!}++\cfrac{x^{2}}{2!}+\cfrac{x^{3}}{3!}+\ldots\)
- la fonction réciproque du logarithme népérien
- la fonction \(f\) telle que \(f' = f\) et \(f(0) = 1\)
Exercices (série 5)
Exercice 5.1
On vous envoie en mission scientifique dans différents univers du multivers (dans lesquels les lois de la physique ne sont pas nécessairement les mêmes que chez nous). On vous demande de décrire la loi de la chute des corps (distance parcourue en fonction du temps) à partir de vos observations
a) Dans le premier univers, vous constatez que la vitesse de chute d’un corps est constante : au bout d’un temps quelconque \(t\), la vitesse est toujours égale à 1m/s
b) Dans le deuxième univers, vous constatez que la vitesse de chute d’un corps est égale au temps de parcours : au bout de 1s sa vitesse est 1m/s, au bout de 2,5s sa vitesse est 2,5m/s, ...
c) Dans le troisième univers, vous constatez que la vitesse de chute d’un corps est égale à 1 plus la distance parcourue : quand il a parcouru 1m sa vitesse est 2m/s, quand il a parcouru 3,5m sa vitesse est 4,5m/s
Dans les trois cas, écrire la distance \(d\) parcourue (en m) en fonction du temps \(t\) (en s) sous la forme \(d=f(t)\) en précisant l’expression de la fonction \(f\)
Exercice 5.2
Pour cet exercice on pourra procéder « à la manière du XVIIème siècle », sans se préoccuper des problèmes de convergence ou d’existence des sommes infinies.
On a une fonction f dont on connnait un développement en série : \(f(x)=1+2x+3x^2+4x^3+5x^4+\ldots\)
a) Quelle est l’aire sous la courbe représentant \(f\) entre \(x=0\) et \(x=\cfrac{1}{2}\) ?
b) Quelle est l’expression algébrique (c’est à dire « sans pointillés ») de \(f\) ?
Complément : intégrale, aire, dérivée, tangente, vitesse
Corrigés
Exercice 5.1
voir corrigé de l’exercice 5.1
corrigé de l’exercice 5.1 (version en ligne)
Exercice 5.2
\(F(x)= \displaystyle{\int f(x).dx=\int 1.dx+\int 2x.dx+\int 3x^2.dx+\ldots=x+x^2+x^3+x^3+\ldots=\cfrac{1}{1-x}-1=\cfrac{x}{1-x}}\)
a) \(aire = F\left(\cfrac{1}{2}\right)=1\)
b) \(f(x)=F'(x)=\cfrac{1}{(1-x)^2}\)
remarque : on peut retrouver ce résultat sans calculer la dérivée, en remarquant que \(f(x)=(1+x+x^2+x^3+\ldots)^2=\left(\cfrac{1}{1-x}\right)^2\)
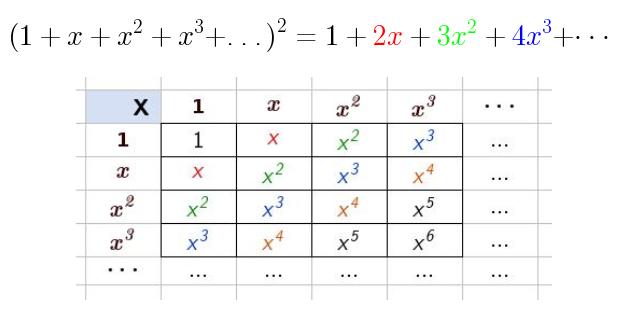
Résumé
La définition de la fonction logarithme népérien provient :
- des tables de logarithmes décimaux qui permettent de remplacer une multiplication par une addition
- de la recherche des fonctions \(L\) qui vérifient : \(L(a\times b)=L(a)\times L(b)\),
- de la mise en évidence du fait que l’aire sous la courbe d’équation \(y=\cfrac{1}{x}\) entre 1 et \(a\) est une fonction du type \(L\) précédent qu’on notera \(\ln\) qui vérifie donc
\(\ln(a\times b)=\ln(a)\times\ln(b)\) et \(\ln(1)=0\)
on peut en déduire que \(\ln\left(\cfrac{a}{b}\right)=\ln(a)-\ln(b)\) et que \(\ln(a^{k})=k\times\ln(a)\)
Il existe donc un nombre, que Euler va noter \(e\) tel que \(\ln(e)=1\) et la question se pose de déterminer sa nature (rationnel, algébrique, transcendant ?) et sa valeur numérique.
On peut remarquer que ceci conduit plus généralement à se poser la question de la définition de la fonction inverse de la fonction \(\ln\),
c’est à dire de trouver une fonction \(E\) qui vérifierait
\(E(x)=y\) si \(y=\ln(x)\),
ainsi que \(E(a+ b)=E(a)\times E(b)\), \(E(a-b)=\cfrac{E(a)}{E(b)}\), \(E(k\times a)=E(a)^{k}\), et \(E(1)=e\)
Enfin, on peut faire le rapprochement avec les fonctions puissances \(x^{n}\) qui vérifient \(x^{m+n}=x^{m}\times x^{n}\), \(x^{m-n}=\cfrac{x^{m}}{x^{n}}\), \(x^{m\times n}=\left(x^{m}\right)^{n}\) et \(x^{1}=x\)
Cette dernière égalité pouvant nous amener au fait que, si \(e\) est connu, on peut écrire \(E(x)=e^x\)
Exercices (série 6)
Exercice 6.1 :
On a vu que les fonctions \(f\) qui vérifient l’équation \(f(xy)=f(x)+f(y)\) pour tout \(x\) et pour tout \(y\) sont les fonctions logarithmes.
et que les fonctions \(f\) qui vérifient l’équation \(f(x+y)=f(x)\times f(y)\) pour tout \(x\) et pour tout \(y\) sont les fonctions exponentielles.
- Trouver toutes les fonctions \(f\) qui vérifient l’équation \(f(x-y)=f(x)\times f(y)\) pour tout \(x\) et pour tout \(y\).
- Trouver toutes les fonctions \(f\) qui vérifient l’équation \(f(x-y)=f(x)\times f(y)\) pour tout \(x\) et pour tout \(y\) distincts.
Exercices 6.2 :
(retour sur les nombres premiers ; cet exercice nécessite d’être à l’aise avec la démonstration par récurrence)
En 1845, Joseph Bertrand émet cette conjecture : étant donné un nombre entier n > 2, il existe toujours un nombre premier p tel que n < p < 2n.
Cette conjecture a été démontrée en 1850 par Chebychev (puis par Ramanujan et enfin par Erdös).
En utilisant cette propriété, résoudre le problème suivant :
Vous vous déplacez en voiture dans le désert d’Algébrie. Les stations de carburant sont numérotées par les nombres premiers :
- la première station (numéro 2) ne peut que vous donner que 2 litres de carburant (que vous prenez pour démarrer)
- la seconde station (numéro 3) ne peut vous donner que 3 litres de carburant, et il vous faudra 1 (= 3 - 2) litres de carburant pour l’atteindre à partir de la station 2
- la troisième station (numéro 5) ne peut vous donner que 5 litres de carburant, et il vous faudra 2 (= 5 - 3) litres de carburant pour l’atteindre à partir de la station 3
- la quatrième station (numéro 7) ne peut vous donner que 7 litres de carburant, et il vous faudra 2 (= 7 - 5) litres de carburant pour l’atteindre à partir de la station 5
- la cinquième station (numéro 11) ne peut vous donner que 11 litres de carburant, et il vous faudra 4 (= 11 - 7) litres de carburant pour l’atteindre à partir de la station 7
De manière générale, si \(p_{n}\) désigne le nième nombre premier, le nième station (de numéro \(p_{n}\)) ne peut vous délivrer que \(p_{n}\) litres de carburant et il vous faudra \(p_{n+1}-p_{n}\) litres de carburant pour atteindre la station suivante (qui a pour numéro \(p_{n+1}\))
Pouvez-vous imaginer, en ayant uniquement 2 litres de carburant en sortant de la station numéro 2, traverser ce désert d’Algébrie (qui est réputé être très grand, infiniment grand peut-être !). Sinon, à quelle station serez-vous contraint à abandonner, faute de carburant ?
Corrigés
Exercice 6.1
Notons d’abord que dans les deux cas, l’égalité \(f(x-y)=f(x).f(y)\) donne, en prenant \(x=0\), \(f(-y)=f(y)\) donc \(f\) est paire.
a) \(f(x-y)=f(x).f(y)\)
En prenant \(y=0\), on obtient : \(f(x)=f(x)\times f(0)\) pour tout \(x\), ce qui donne
- ou bien \(f(x)=0\) pour tout \(x\) (ce qui est une première solution au problème)
- ou bien \(f(0)=1\)
Supposons maintenant \(f(0)=1\)
Notons \(m=\cfrac{x+y}{2}\) et \(d=\cfrac{y-x}{2}\) ; alors \(x=m-d\) et \(y=m+d=m-(-d)\) ;
\(f(x)=f(m-d)=f(m).f(d)\)
\(f(y)=f(m-(-d))=f(m).f(-d)=f(m).f(d)\) car \(f\) est paire
donc \(f(x)=f(y)\) pour tous réels \(x\) et \(y\), c’est à dire que \(f\) est constante ; comme \(f(0)=1\), on en déduit que \(f(x)=1\) pour tout \(x\)
On vérifie réciproquement que les seules solutions sont bien \(f=0\) et \(f=1\)
b)
La partie du raisonnement ci-dessus faisant intervenir \(m\) et \(d\) reste valable si \(m\neq d\) et \(m\neq -d\), c’est à dire si \(x\ne 0\) et \(y\neq 0\) ; on en déduit que \(f\) est constante sur \(\mathbb{R}-\{0\}\).
Donc il existe deux constantes \(a\) et \(b\) telles que
\(f(0)=a\) et \(f(x)=b\) si \(x\neq 0\)
\(b=f(1)=f(2-1)=f(2)\times f(1)=b^2\) donc \(b=0\) ou \(b=1\)
- si \(b=1\) : \(1=f(1)=f(1-0)=f(1)\times f(0)=f(0)\) donc \(f=1\)
- si \(b=0\) : on vérifie que toute fonction nulle sur \(\mathbb{R}-\{0\}\) convient
Exercice 6.2
Une première réponse, réaliste : comme le réservoir de la voiture à une contenance limitée et que les écarts entre les nombres premiers consécutifs peuvent être aussi grands que l’on veut, il y aura un moment où la contenance totale du réservoir sera inférieure à la différence des numéros entre la prochaine station et celle où l’on se trouve, c’est à dire à la quantité de carburant nécessaire pour parcourir la prochaine étape !
Sinon, ... :
On note \(p_k\) le \(k^{ieme}\) nombre premier, avec \(p_1=2\).
Quand on quitte la station \(p_1\) on a une quantité de carburant égale à \(p_{1}\)
Pour aller à la station \(p_{2}\) on utilise la quantité \(p_{2}-p_{1}\) de carburant, il nous en reste \(p_{1}-(p_{2}-p_{1})=2.p_{1}-p_{2}\) en arrivant à la station \(p_{2}\) où on en prend une quantité \(p_{2}\) donc on quitte la station \(p_{2}\) avec une quantité de carburant égale à \(2.p_{1}\)
De même
- on quitte la station \(p_{3}\) avec une quantité de carburant égale à \(2.p_{1}-(p_{3}-p_{2})+p_{3}=2.p_{1}+p_{2}\)
- on quitte la station \(p_{4}\) avec une quantité de carburant égale à \((2.p_{1}+p_{2})-(p_{4}-p_{3})+p_{4}=2.p_{1}+p_{2}+p_{3}\)
Hypothèse de récurrence : on quitte la station \(p_{n}\) avec une quantité de carburant égale à \(2.p_{1}+p_{2}+p_{3}+\ldots + p_{n-1}\) (propriété A)
en lui retranchant la quantité consommée puis en lui ajoutant la quantité reçue à la station \(p_{n+1}\) on obtient \(2.p_{1}+p_{2}+p_{3}+\ldots+p_{n-1}-(p_{n+1}-p_{n})+p_{n+1}=2.p_{1}+p_{2}+p_{3}+\ldots+p_{n-1}+p_{n}\), ce qui démontre la propriété (A) à l’ordre \(n+1\).
Reste à démontrer que cette quantité de carburant \(2.p_{1}+p_{2}+p_{3}+\ldots + p_{n-1}\) permet d’atteindre la station suivante, trajet pendant lequel la consommation est \(p_{n+1}-{p_{n}}\)
Il faut donc que l’inégalité \(p_{n+1}-p_{n}\leq2.p_{1}+p_{2}+p_{3}+\ldots + p_{n-1}\) soit vraie, ce qui s’écrit \(p_{n+1}\leq2.p_{1}+p_{2}+p_{3}+\ldots+p_{n}\) (propriété B)
Hypothèse de récurrence : \(p_{n+1}\leq2.p_{1}+p_{2}+p_{3}+\ldots + p_{n}\)
pour \(n = 1\) : \(p_2 \leq 2\times p_{1}\) soit \(3 \leq 2\times 2\) (vrai)
D’après le théorème de Bertrand, il existe toujours un nombre premier \(p\) tel que \(p_{n+1} < p < 2.p_{n+1}\) ; en particulier on en déduit que \(p_{n+1} < p_{n+2}\leq 2.p_{n+1}\)
Donc \(p_{n+2} \leq 2p_{n+1} =p_{n+1} + p_{n+1} \leq (2.p_{1}+p_{2} + \ldots + p_{n}) + p_{n+1}\) (hypothèse de récurrence)
D’où \(p_{n+2}\leq2.p_{1}+p_{2}+\ldots + p_{n} + p_{n+1}\) ce qui démontre la propriété B
Donc on peut sans crainte traverser le désert d’Algébrie jusqu’à l’infini et au-delà !
Les nombres complexes
Une brève histoire des équations
Le second degré
Bien avant l’invention de l’algèbre par Al-Khwarizmi au VIIIème siècle, les mathématiciens mésopotamiens, grecs, chinois, ... ont réussi à résoudre des problèmes qu’on interpréterait maintenant comme étant des problèmes conduisant à une équation du second degré.
Exemple (type Euclide, IIIème siècle av. J.-C.) : second degré
Actuellement on dit que les solutions de l’équation \(ax^{2}+bx+x=0\) sont données par \(x=\cfrac{-b+\sqrt{b^{2}-4ac}}{2a}\) ou \(x=\cfrac{-b-\sqrt{b^{2}-4ac}}{2a}\) si \(b^{2}-4ac\geq0\).
Les Grecs avaient remarqué que dans certains cas ces problèmes conduisaient à obtenir un carré d’aire négative. Ils considéraient alors qu’il n’y avait pas de solution.
L’invention de l’algèbre

En créant le concept d’inconnue (Diophante : l’arithme, IIIème siècle après J.-C. puis Al-Khwarizmi : la chose, IXème siècle) les mathématiciens grecs d’Alexandrie, puis les mathématiciens arabo-musulmans de Bagdad vont inventer l’algèbre.
Al-Khwarizmi va classer les 6 types d’équations du second degré connues (ceci est rendu nécessaire par l’incapacité à utiliser des coefficients négatifs) puis Omar Khayyam au XIème siècle va classer de la même manière les 13 types d’équations du troisième degré, sans toutefois parvenir à en trouver les solutions dans le cas général.
Del Ferro, Tartaglia
Vers 1510, à Bologne, Del Ferro réussit à trouver des formules pour les équations du type \(x^{3}+px+q=0\) mais ne communique pas ses résultats, en raison de la concurrence entre les mathématiciens à l’époque. En 1535 à Venise, Tartaglia (Nicolao Fontana) retrouve ces formules en reprenant l’idée consistant à compléter le développement d’un carré ou d’un cube :
Exemple : \(x^3+9x=26\)
Tartaglia : équation du troisième degré
Cardan, Bombelli

Tartaglia a écrit sous forme de poème l’algorithme permettant de calculer les solutions des équations du second degré (voir ci-contre, avec leur traduction algébrique actuelle).
Mais il ne diffuse pas ces formules que finalement Cardan va réussir à lui « soutirer » en mars 1539 à Milan.
Cardan va étendre les formules aux équations \(ax^{3}+bx^{2}+cx+d=0\) par le changement de variable \(x\longrightarrow x-\cfrac{b}{3a}\)
Bombelli, en s’attaquant à l’équation \(x^{3}=15x+4\) s’aperçoit aisément qu’elle a comme solution \(x=4\) ; cependant les formules de Cardan et Tartaglia pour cette équation s’écrivent \(x=\sqrt[3]{2+\sqrt{-121}}+\sqrt[3]{2-\sqrt{-121}}\) et semblent prouver que cette équation n’a pas de solution.
Il fait abstraction de cette impossibilité (qui correspondrait à l’existence d’un carré d’aire égale à -121) et, en écrivant \(\sqrt{-121}\) sous la forme \(11\sqrt{-1}\) il obtient :
\(x = \sqrt[3]{2+11\sqrt{-1}}+\sqrt[3]{2-11\sqrt{-1}}\)
et enfin en développant \((2-\sqrt{-1})^3=2-11\sqrt{-1}\) il obtient \(\sqrt[3]{2-11\sqrt{-1}}=2-\sqrt{-1}\)
et en développant \((2+\sqrt{-1})^3=2+11\sqrt{-1}\) il obtient \(\sqrt[3]{2+11\sqrt{-1}}=2+\sqrt{-1}\)
Finalement \(x = \sqrt[3]{2+\sqrt{-121}}+\sqrt[3]{2-\sqrt{-121}} = 2+\sqrt{-1}+2-\sqrt{-1}=4\)
Il appelle ces nombres des nombres imaginaires.
Conclusion

En termes modernes, on peut dire que le grand apport de Bombelli a été d’accepter de travailler sur des « nombres », qu’on appellera d’abord imaginaires, de la forme \(a+b\sqrt{-1}\), avec \(a\) et \(b\) réels.
Euler, au XVIIIème siècle, introduira la notation \(i\) pour \(\sqrt{-1}\) et on appellera les nombres de la forme \(a+bi\) des nombres complexes.
À travers cet abandon de l’intuition, l’invention des nombres complexes permettra à l’algèbre de se développer pour résoudre des problèmes très généraux de manière efficace. La compréhension de la nature de ces nombres imaginaires ou complexes progressera en en donnant une interprétation géométrique.
Au XXème siècle, ces nombres vont s’avérer incontournables dans la description du monde réel qu’en donne la mécanique quantique. Les propriétés des objets de cette physique et les équations (équation de Schrödinger par exemple) font intervenir des nombres complexes.
Considérations « philosophiques »
Cette histoire peut être l’occasion de poser cette question propre à la philosophie mathématique : ces nombres complexes sont-ils découverts ou construits (inventés) ?
La position platonicienne (réalisme platonicien)
« Outre l’existence des choses sensibles et des Idées, Platon admet celle des Choses mathématiques [Nombres, Lignes, Surfaces, Solides], qui sont des réalités intermédiaires, différentes, d’une part, des Choses sensibles, en ce qu’elles sont éternelles et immobiles, et, d’autre part, des Idées, en ce qu’elles sont une pluralité d’exemplaires semblables, tandis que l’Idée est en elle-même une réalité une, individuelle et singulière. »
[Aristote, Métaphysique, vers 350 av. J.-C.]
Remarque : Aristote, en fait, soutient le point de vue opposé à celui de Platon : il n’y a pas de monde mathématique en soi; si l’on en parle, c’est en tant qu’idées abstraites de l’activité humaine, à savoir des constructions des mathématiciens créateurs.
« La structure d’une chose n’est nullement une chose que nous puissions « inventer ». Nous pouvons seulement la mettre à jour patiemment, humblement en faire connaissance, la « découvrir ». S’il y a inventivité dans ce travail, et s’il nous arrive de faire œuvre de forgeron ou d’infatigable bâtisseur, ce n’est nullement pour « façonner », ou pour « bâtir », des « structures ». Celles-ci ne nous ont nullement attendues pour être, et pour être exactement ce qu’elles sont ! Mais c’est pour exprimer, le plus fidèlement que nous le pouvons, ces choses que nous sommes en train de découvrir et de sonder, et cette structure réticente à se livrer, que nous essayons à tâtons, et par un langage encore balbutiant peut-être, à cerner. »
[A. Grothendieck, Récoltes et semailles, 1985]
À l’opposé le constructivisme est une philosophie des mathématiques définie par deux composantes :
- au plan ontologique, le constructiviste considère les objets mathématiques, non comme existant « par eux-mêmes », mais comme le résultat des constructions mentales du mathématicien
- au plan méthodologique, il insiste sur l’importance des preuves dites « constructives », c’est-à-dire des démonstrations qui, si elles concluent à l’existence d’un objet, donnent une méthode permettant d’en produire effectivement un exemplaire, au lieu de se contenter d’établir que l’inexistence de l’objet conduirait à une contradiction
Genèse algébrique de l’ensemble des nombres complexes
On essaie d’ajouter \(i\) à l’ensemble \(\mathbb{R}\) des nombres réels de manière à ce que les propriétés de l’addition et de la multiplication dans \(\mathbb{R}\) soient préservées.
Opérations internes : on doit pouvoir additionner, soustraire, multiplier, diviser des expressions algébriques contenant des nombres complexes ou réels et obtenir des nombres complexes ou réels.
Donc doivent exister, en tant que nombres réels ou complexes toutes les expressions de la forme \(\cfrac{\alpha_{n}p^{n}+\alpha_{n-1}p^{n-1}+\ldots+\alpha_1p+\alpha_0}{\beta_{n}q^{n}+\beta_{n-1}q^{n-1}+\ldots+\beta_1q+\beta_0}\) faisant intervenir des nombres \(\alpha_{i}\), \(\beta_{j}\), \(p\) et \(q\) réels ou complexes.
La pratique des calculs met en évidence qu’il suffit de supposer que tout nombre complexe \(z\) s’écrit sous la forme \(z=a+bi\) avec \(a\) et \(b\) réels et \(i^{2}=-1\)
Le théorème général de l’algèbre
Théorème de d’Alembert-Gauss (1815) : tout polynôme \(P\) non constant à coefficients complexes admet au moins une racine complexe.
Conséquence : pour tout polynôme \(P\) non constant de degré \(n\) à coefficients complexes, l’équation \(P(z)=0\) possède exactement \(n\) racines complexes (en comptant leur ordre de multiplicité).
On dit que le corps \(\mathbb{C}\) des nombres complexes est algébriquement clos.
Exemples
\(z^2+1=0\) possède 2 solutions : \(i\) et \(-i\)
\(z^{2}-1=0\) possède 2 solutions : 1 et -1
\(z^{3}-1=0\) possède 3 solutions : 1, \(\cfrac{1+i\sqrt{3}}{2}\) et \(\cfrac{1-i\sqrt{3}}{2}\)
\(z^{4}+2z^{2}+1=0\) possède deux solutions doubles \(i\) et \(-i\)
\(z^{2}-i=0\) possède deux solutions \(\sqrt{i}=\cfrac{\sqrt{2}}{2}+i\cfrac{\sqrt{2}}{2}\) et \(-\sqrt{i}\)
Remarque
Ce théorème ne possède pas de démonstration purement algébrique. À un certain moment de la démonstration il est nécessaire d’invoquer des arguments d’analyse liés aux limites ou à la continuité.
Ce théorème démontre l’existence des solutions mais ne permet pas de les calculer.
Clôture algébrique de \(\mathbb{C}\)
Genèse géométrique des nombres complexes
On a vu que l’introduction des nombres complexes amène à considérer un corps de nombres de la forme \(a+bi\), ce qui peut être interprété comme l’extension des opérations habituelles (dans \(\mathbb{R})\) au couples \((a,b)\) de réels, c’est à dire aux points du plan.
Coordonnées cartésiennes
addition des nombres complexes
multiplication des nombres complexes
En coordonnées cartésiennes l’interprétation de l’addition des nombres complexes est assez intuitive ; ce n’est pas du tout le cas pour la multiplication.
Coordonnées polaires
Exponentielle complexe
On a remarqué que multiplier deux nombres complexes revient à additionner leurs arguments et multiplier leurs modules
En coordonnées polaires : si \(z_1=[r_1, a_1]\) et \(z_2=[r_2, a_2]\) alors \(z_1.z_2=[r_1.r_2, a_1+a_2\)]
Ceci suggère une analogie avec les formules du type \(r_1.e^{a_1}\times r_2.e^{a_2}=r_1.r_2.e^{a_1+a_2}\)
Au XVIIIème siècle, de Moivre et surtout Euler, suite aux progrès liés à l’étude de l’exponentielle et des développement en séries infinies des fonctions trigonométriques vont parvenir à construire la notation exponentielle pour les nombres complexes :
Un nombre complexe \(z=x+iy\) qui a pour module \(r\) et pour argument \(a\) peut s’écrire sous la forme \(z=r(\cos a+i.\sin a)\) (forme trigonométrique). Mais les remarques précédentes sur la multiplication des complexes en coordonnées polaires rendent cohérente la notation \(z=re^{ia}\).
Les règles de cette addition se démontrent en utilisant les formules d’addition des fonctions trigonométriques.
La célèbre formule d’Euler : \(e^{i\pi}=-1\) s’en déduit : elle signifie simplement qu’une rotation de centre O et d’angle \(\pi\) (en radians, c’est à dire 180°) n’est autre qu’une symétrie par rapport à O.
Les racines nièmes de l’unité 20240503
Dans l’ensemble des nombres réels, l’équation \(x^{2}-2=0\) possède deux solutions : c’est la solution positive qu’on note \(\sqrt{2}\), l’autre étant \(-\sqrt{2}\).
Dans l’ensemble des nombres complexes, l’équation \(x^{2}+1=0\) possède deux solutions, mais on ne peux plus en déterminer une en disant qu’elle est positive ; on note arbitrairement l’une d’elle \(i\) ; l’autre étant alors \(-i\).
Dans l’ensemble des nombres réels, l’équation \(x^3-1=0\) possède une seule solution \(x=1\)
Mais dans l’ensemble des complexes, cette équation possède 3 solutions : une réelle (1) et deux complexes conjuguées (\(\cfrac{-1+i\sqrt{3}}{2}\) et \(\cfrac{-1-i\sqrt{3}}{2}\)) : 1 possède trois racines cubiques.
racines cubiques de l’unité
Les fonctions racines dans \(\mathbb{C}\) sont donc « multivaluées » : il n’est pas possible de choisir une valeur déterminée pour les racines comme on le fait pour les nombres réels dans lesquels on choisit comme racine nième d’un réel positif \(A\) le nombre positif \(a\) tel que \(a^{n}=A\) (de même si \(A<0\), on choisit peut choisir la valeur négative de \(a\));
pour les nombres complexes la notion de positivité n’existe pas (il n’y a pas de relation d’ordre dans \(\mathbb{C}\)) : par exemple il n’est pas possible de choisir entre \(i\) et \(-i\) pour la racine carrée de \(-1\).
complexes et polygones réguliers
Interprétation des transformations du plan
Intersections imaginaires
En 1750 Euler se pose la question du nombre de points d’intersection de 2 courbes algébriques dans le plan complexe ; en 1764 Étienne Bezout démontre que deux courbes algébriques de degrés \(m\) et \(n\) ont exactement \(mn\) points (éventuellement multiples) d’intersection, en comptant les points à coordonnées complexes et les points à l’infini (c’est à dire en se plaçant dans le plan projectif complexe). Au début du XIXème siècle, Lazare Carnot, Jean Victor Poncelet, Georg von Staudt et Michel Chasles vont essayer de représenter les éléments « imaginaires » intervenant dans l’étude de l’intersection des coubes. Ils utilisent pour cela l’interprétation géométrique des nombres complexes donnée par Caspar Wessel en 1797 et Jean-Robert Argand en 1806.
Exemple : que deviennent les points d’intersection (réels) de deux cercles quand ces cercles ne ne coupent plus ? : intersection de 2 cercles dans le plan complexe
Les fonctions d’une variable complexe
Le vocabulaire des fonctions d’une variable réelle, qui s’est développé tout au long du XVIIème et du XVIIIème siècle, va s’étendre à la variable complexe.
Comment représenter une fonction \(f:\mathbb{C}\longrightarrow\mathbb{C}\) ?
La manière de se représenter les « espaces » et de représenter les fonctions est liée à notre position d’être humain dans l’espace physique de dimension 3.
Nous représentons une fonction \(f:\mathbb{R}\longrightarrow\mathbb{R}\) dans un repère cartésien du plan parce que :
- l’axe réel \(\mathbb{R}\) est un espace de dimension 1
- le plan cartésien (produit cartésien de 2 axes) est de dimension 2
- l’intersection des axes cartésiens est un point
- notre position en dimension 3 nous permet d’être « en surplomb » de ce plan
De même, nous sommes capables de représenter des fonctions en dimension 3 parce que :
- nous les représentons en les projetant sur une plan de dimension 2
- l’intersection des 3 axes est un point
Par contre, on ne peut pas (se) représenter un espace de dimension 4 : il faudrait que nous ayons une position visuelle de surplomb dans cet espace sur les espaces de dimension 3.
Imaginons un mathématicien extra-terrestre infiniment plat (de dimension 2 ) vivant dans un espace de dimension 2. Comment peut-il envisager de représenter la fonction \(f\) définie par \(f(x)=x^{2}\) ?
Une solution : il représente sur une droite, en chaque point d’abscisse \(x\), la valeur de \(f(x)\) par une couleur. (avec une convention permettant d’associer une couleur ou un niveau de gris à chaque réel)
flatland
Représentation à l’aide de deux plans
Représentation séparée des parties réelles et imaginaires
séparation de la partie réelle et de la partie imaginaire :
On représente une fonction \(f:\mathbb{C} \rightarrow \mathbb{C}\) par deux fonctions \(Re(f):\mathbb{C} \rightarrow \mathbb{R}\) et \(Im(f):\mathbb{C} \rightarrow \mathbb{R}\)
représentation des parties réelles et imaginaires
Représentation à l’aide de couleurs
On va colorier chaque point \(z\) du plan complexe à l’aide d’une couleurs associée à la valeur de \(w=f(z)\).
Pour chaque nombre complexe \(w=re^{i\theta}\) le couleur va dépendre du module \(r\) et de l’argument \(\theta\), en utilisant le cercle chromatique des couleurs.
représentation chromatique
voir aussi : http://localhost:8888/lab/tree/utl/atelier%20informatique/01-programmation%20en%20python/fonction%20complexe.ipynb (jupyterlab)
Champs de vecteurs
Quaternions
Le 16 octobre 1843, Hamilton, après plusieurs années de recherche vaine d’une extension de l’idée du « plan complexe » à l’espace de dimension 3, découvre que c’est possible dans un espace de dimension 4 en écrivant les quaternions sous la forme \(a+bi+cj+dk\) où \(a\), \(b\), \(c\) et \(d\) sont des nombres réels et \(i\), \(j\) et \(k\) sont des symboles vérifiant \(i^{2}=j^{2}=k^{2}=ijk=-1\).
L’ensemble \(\mathbb{H}\) est un corps non commutatif :
par exemple : \(ijk=-1 \implies ijkk=-k \implies -ij=-k\) (car \(kk=k^{2}=-1\)) donc \(ij=k\)
mais \(ijk=-1 \implies iijk=-i \implies -jk=-i \implies jk=i \implies jjk=ji \implies -k=ji\)
donc \(ji=-ij\).
Le rôle qu’aurait pu jouer les quaternions dans les espaces de dimension 4 qui vont être utilisés par Einstein un demi-siècle plus tard va être éclipsé par l’utilisation du calcul vectoriel.
Octonions
Le 16 octobre 1843, Hamilton envoie une lettre de huit pages à son ami Graves lui faisant part de sa découverte ; le 26 décembre Graves étend l’idée de Hamilton dans un espace de dimension 8 noté \(\mathbb{O}\) dont les éléments sont appelés octonions. On peut les écrire sous la forme
\(a+be_{1}+ce_{2}+de_{3}+ee_{4}+fe_{5}+ge_{6}+he_{7}\)
La multiplication des octonions n’est pas associative : si \(\alpha\), \(\beta\) et \(\gamma\) sont trois octonions, alors, en général \((\alpha\beta)\gamma\neq\alpha(\beta\gamma)\).
